|
Question 389130: 1.Solve each system of equations using the elimination method.11x + 16y = 922x + 3y = 18
2.Solve each system of equations using the substitution method. 4x - y = 32y = -2 x + 70
3.Rewrite the linear programming problem as a maximization problem with constraints involving inequalities of the form≤ a constant (with the exception of the inequalities x≥0, y≥0, and z ≥0).
Minimize C = 2x-3y
Subject to 3x +5y ≥20
3x+y≤16
-2x+y≤1
x≥0, y≥0
4. Find the distance between P and Q.P ( -8 , -9 ) and Q ( 10 , -9 )
5.Find the distance between P and Q. P ( -9 , -5 ) Q ( 9 , -21 )
6.Write an equation of the line that passes through the given two points ( -2 , 7 ), ( 4 , -23 )
*[invoke calculating_slope -2, 7, 4, -23]
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
1.Solve each system of equations using the elimination method.

 .....I guess this is your system.... .....I guess this is your system....
| Solved by pluggable solver: Solving a System of Linear Equations by Elimination/Addition |
Lets start with the given system of linear equations


In order to solve for one variable, we must eliminate the other variable. So if we wanted to solve for y, we would have to eliminate x (or vice versa).
So lets eliminate x. In order to do that, we need to have both x coefficients that are equal but have opposite signs (for instance 2 and -2 are equal but have opposite signs). This way they will add to zero.
So to make the x coefficients equal but opposite, we need to multiply both x coefficients by some number to get them to an equal number. So if we wanted to get 11 and 2 to some equal number, we could try to get them to the LCM.
Since the LCM of 11 and 2 is 22, we need to multiply both sides of the top equation by 2 and multiply both sides of the bottom equation by -11 like this:
 Multiply the top equation (both sides) by 2 Multiply the top equation (both sides) by 2
 Multiply the bottom equation (both sides) by -11 Multiply the bottom equation (both sides) by -11
So after multiplying we get this:


Notice how 22 and -22 add to zero (ie  ) )
Now add the equations together. In order to add 2 equations, group like terms and combine them


 Notice the x coefficients add to zero and cancel out. This means we've eliminated x altogether. Notice the x coefficients add to zero and cancel out. This means we've eliminated x altogether.
So after adding and canceling out the x terms we're left with:

 Divide both sides by Divide both sides by  to solve for y to solve for y
 Reduce Reduce
Now plug this answer into the top equation  to solve for x to solve for x
 Plug in Plug in 
 Multiply Multiply
 Subtract Subtract 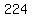 from both sides from both sides
 Combine the terms on the right side Combine the terms on the right side
 Multiply both sides by Multiply both sides by  . This will cancel out . This will cancel out  on the left side. on the left side.
 Multiply the terms on the right side Multiply the terms on the right side
So our answer is
 , , 
which also looks like
( , ,  ) )
Notice if we graph the equations (if you need help with graphing, check out this solver)


we get
 graph of graph of  (red) (red)  (green) (hint: you may have to solve for y to graph these) and the intersection of the lines (blue circle). (green) (hint: you may have to solve for y to graph these) and the intersection of the lines (blue circle).
and we can see that the two equations intersect at ( , , ). This verifies our answer. ). This verifies our answer. |
2.Solve each system of equations using the substitution method.

 ..or.. ..or..
| Solved by pluggable solver: SOLVE linear system by SUBSTITUTION |
Solve:
 We'll use substitution. After moving -1*y to the right, we get: We'll use substitution. After moving -1*y to the right, we get:
 , or , or  . Substitute that . Substitute that
into another equation:
 and simplify: So, we know that y=36. Since and simplify: So, we know that y=36. Since  , x=17. , x=17.
Answer:  . .
|
4. Find the distance between P and Q.P ( -8 , -9 ) and Q ( 10 , -9 )
| Solved by pluggable solver: Finding a distance between a point given by coordinates (x, y) and a line given by equation y=ax+b |
We want to find the perpendicular distance between a point given by coordinates ( , , ) )
and a line given by equation 
First, let's draw a diagram of general situation with point P (xo, yo) and
line L: y= a.x + b. The required distance is PC. (in the diagram below)

Methodology
We will first find the vertices of the triangle in order to get the side lengths and then by applying
Sine Rule on right angle triangle PAB and PBC we will calculate the desired distance PC.
Step1
Calculation of the vertices of triangle PAB:
Draw a vertical line passing through the point 'P'. This line  will cut the given line 'L' will cut the given line 'L'
at point 'A'. The X coordinate of A(x1) will be same as  . To find the Y-coordinate of . To find the Y-coordinate of
'A' we will use the fact that point 'A' lies on the given line 'L' and satisfies the equation
of the line 'L' .
Now, plug this  in to the equation of line: y=10*x+-9 in to the equation of line: y=10*x+-9


Hence, Point (A)( , , ) )
Similarly,
Draw a horizontal line passing through the point 'P'. This line  will cut the given line 'L' will cut the given line 'L'
at point 'B'. The Y coordinate of B(y2) will be same as  . To find the X-coordinate of . To find the X-coordinate of
B we will use the fact that point 'B' lies on the given line 'L' and satisfies the equation
of the line 'L' .
Now, plug this  in to the equation of line: y=10*x+-9 in to the equation of line: y=10*x+-9



Hence, Point (B)( , , ) )
Now, we have all the vertices of the triangle PAB
Step2
Calculation of the side lengths using distance formula:

Hence, The side lengths PA, PB and AB are



Step3
Apply Sine rule on common angle B in triangle PAB and triangle PBC.
Both triangle PAB and triangle PBC are right angle triangle and points 'A', 'B' and 'C' lay on the given line L.


PC is the required perpendicular distance of the point P (-8, -9) from line given
lineL1: y=10*x+-9.
For better understanding of this concept, look at the Lesson based on the above concept.
Lesson |
5.Find the distance between P and Q. P ( -9 , -5 ) Q ( 9 , -21 )
| Solved by pluggable solver: Finding a distance between a point given by coordinates (x, y) and a line given by equation y=ax+b |
We want to find the perpendicular distance between a point given by coordinates ( , , ) )
and a line given by equation 
First, let's draw a diagram of general situation with point P (xo, yo) and
line L: y= a.x + b. The required distance is PC. (in the diagram below)

Methodology
We will first find the vertices of the triangle in order to get the side lengths and then by applying
Sine Rule on right angle triangle PAB and PBC we will calculate the desired distance PC.
Step1
Calculation of the vertices of triangle PAB:
Draw a vertical line passing through the point 'P'. This line  will cut the given line 'L' will cut the given line 'L'
at point 'A'. The X coordinate of A(x1) will be same as  . To find the Y-coordinate of . To find the Y-coordinate of
'A' we will use the fact that point 'A' lies on the given line 'L' and satisfies the equation
of the line 'L' .
Now, plug this  in to the equation of line: y=9*x+-21 in to the equation of line: y=9*x+-21


Hence, Point (A)( , , ) )
Similarly,
Draw a horizontal line passing through the point 'P'. This line  will cut the given line 'L' will cut the given line 'L'
at point 'B'. The Y coordinate of B(y2) will be same as  . To find the X-coordinate of . To find the X-coordinate of
B we will use the fact that point 'B' lies on the given line 'L' and satisfies the equation
of the line 'L' .
Now, plug this  in to the equation of line: y=9*x+-21 in to the equation of line: y=9*x+-21



Hence, Point (B)( , , ) )
Now, we have all the vertices of the triangle PAB
Step2
Calculation of the side lengths using distance formula:

Hence, The side lengths PA, PB and AB are



Step3
Apply Sine rule on common angle B in triangle PAB and triangle PBC.
Both triangle PAB and triangle PBC are right angle triangle and points 'A', 'B' and 'C' lay on the given line L.


PC is the required perpendicular distance of the point P (-9, -5) from line given
lineL1: y=9*x+-21.
For better understanding of this concept, look at the Lesson based on the above concept.
Lesson |
6.Write an equation of the line that passes through the given two points
( -2 , 7 ), ( 4 , -23 )
| Solved by pluggable solver: Finding the Equation of a Line |
First lets find the slope through the points ( , , ) and ( ) and ( , ,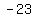 ) )
 Start with the slope formula (note: ( Start with the slope formula (note: ( , , ) is the first point ( ) is the first point ( , , ) and ( ) and ( , , ) is the second point ( ) is the second point ( , ,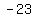 )) ))
 Plug in Plug in  , , , , , , (these are the coordinates of given points) (these are the coordinates of given points)
 Subtract the terms in the numerator Subtract the terms in the numerator 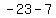 to get to get  . Subtract the terms in the denominator . Subtract the terms in the denominator 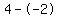 to get to get 
 Reduce Reduce
So the slope is

------------------------------------------------
Now let's use the point-slope formula to find the equation of the line:
------Point-Slope Formula------
 where where  is the slope, and ( is the slope, and ( , , ) is one of the given points ) is one of the given points
So lets use the Point-Slope Formula to find the equation of the line
 Plug in Plug in  , ,  , and , and  (these values are given) (these values are given)
 Rewrite Rewrite 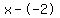 as as 
 Distribute Distribute 
 Multiply Multiply  and and  to get to get 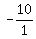 . Now reduce . Now reduce 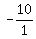 to get to get 
 Add Add  to both sides to isolate y to both sides to isolate y
 Combine like terms Combine like terms  and and  to get to get 
------------------------------------------------------------------------------------------------------------
Answer:
So the equation of the line which goes through the points ( , , ) and ( ) and ( , ,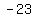 ) is: ) is:
The equation is now in  form (which is slope-intercept form) where the slope is form (which is slope-intercept form) where the slope is  and the y-intercept is and the y-intercept is 
Notice if we graph the equation  and plot the points ( and plot the points ( , , ) and ( ) and ( , ,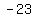 ), we get this: (note: if you need help with graphing, check out this solver) ), we get this: (note: if you need help with graphing, check out this solver)
 Graph of Graph of  through the points ( through the points ( , , ) and ( ) and ( , ,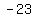 ) )
Notice how the two points lie on the line. This graphically verifies our answer.
|
|
|
|
| |