|
Question 350822: I need help with this problem: Determine whether the lines with the given slopes are parallel, perpendicular or neither. The slope given is: m1=3,
m2= -1/3. I don't know how to set up the equation in order to find the solution. I know that parallel lines will have the same slope and that perpendicular lines will have negative reciprocals, but without being given the x and y axis, how can I set this up to find out the points of the two lines?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! since you are given the slopes, and you know that parallel lines have the same slope and you know that perpendicular lines, all you have to do is examine the slopes and you will have your answer.
you do not have to set up and i will show you why.
the slope of the first line is 3
the slope of the second line is -1/3
the negative reciprocal of 3 is -1/3 so the lines have to be perpendicular.
if you want to draw these lines, you can actually place them anywhere on the graph and it will show you the relationship.
the only problem you would have is if the lines were parallel.
in that case, the equation would have to have a different y-intercept.
otherwise they would be the same line.
the equation of a straight line in slope intercept form is:
y = mx + b
you have m, so replace m with your slope and you will get:
y = 3x + b
and:
y = -1/3x + b
b is your y-intercept.
replace b with anything reasonable.
let's use b = 3 for both equations.
your equations become:
y = 3x + 3
y = -1/3x + 3
all this means is that both lines will cross the y-axis at y = 3
the graphs of both these equations are shown below:
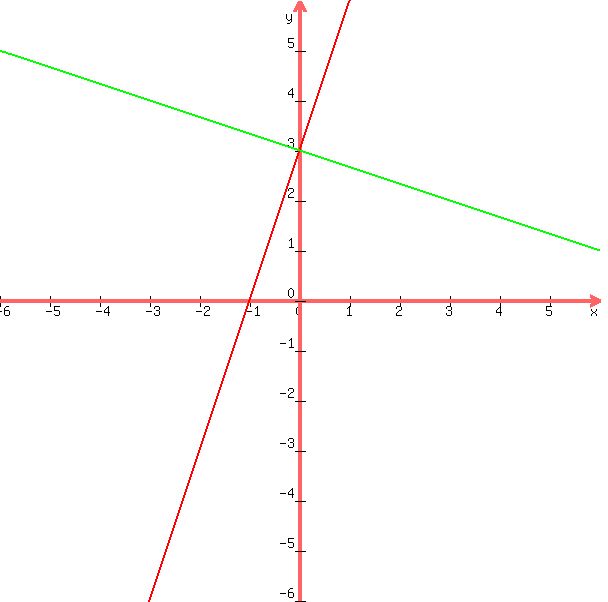
you can see that the lines are perpendicular to each.
that's because the slopes are negative reciprocals to each other.
suppose the lines were parallel.
the slope would have then been the same.
you would have had:
y = 3x + b
y = 3x + b
in this case, the b value could not be the same.
if it was the lines would be identical.
we'll make the b values different to show you that they are parallel.
the equations we'll use are:
y = 3x + 3
y = 3x + 6
the graph of those equations are shown below:

you can see that these lines are parallel.
if the b values were the same, both lines would collapse into one line because they would be super-imposed on each other.
i'll bring b values closer but not exactly the same so you can see that.
the equations i'll use are:
y = 3x + 3
y = 3x + 2.8
the graph of these equations will look like this:

you can see that if i made the b value the same, these 2 lines would look like one line.
in such a case, they would be called identical and not parallel.
parallel lines have the same slope but a different b value.
identical lines have the same slope and the same b value.
the fact that they are parallel or perpendicular has to do with the slope only.
you could replace the b value with anything you want and the lines would still be parallel or perpendicular depending on whether the slopes were the same or negative reciprocals of each other.
the only caveat is that the parallel lines would have to have a different b value (y-intercept).
for your problem, i'll replace the b values as follows.
y = 3x + 3
y = -(1/3)x - 3
the graph of these 2 equations is shown below:

the lines are cross the y-axis at different points, but they are still perpendicular to each other.
|
|
|
| |