SOLUTION: anyone but john please help with question. Solve the following ssystem of equation xy=1 2x-y=1

Algebra ->  Linear-equations -> SOLUTION: anyone but john please help with question. Solve the following ssystem of equation xy=1 2x-y=1      Log On


   

Question 331485: anyone but john please help with question. Solve the following ssystem of equation xy=1
2x-y=1
Found 2 solutions by JBarnum, Edwin McCravy:
Answer by JBarnum(2146) About Me  (Show Source):
You can put this solution on YOUR website!
lol anyone but john...lol he must of gave u a bad answer..lol
2x-y=1
2x=1%2By
%282x-1%29=y substitute this in other equation


x%282x-1%29=1
2x%5E2-x=1
2x%5E2-x-1=0 View quadratic equation below
x=1,-0.5
to find y simply plug in the x's
y=1,0

Solved by pluggable solver: SOLVE quadratic equation with variable
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 2x%5E2%2B-1x%2B-1+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-1%29%5E2-4%2A2%2A-1=9.

Discriminant d=9 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28--1%2B-sqrt%28+9+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%28-1%29%2Bsqrt%28+9+%29%29%2F2%5C2+=+1
x%5B2%5D+=+%28-%28-1%29-sqrt%28+9+%29%29%2F2%5C2+=+-0.5

Quadratic expression 2x%5E2%2B-1x%2B-1 can be factored:
2x%5E2%2B-1x%2B-1+=+2%28x-1%29%2A%28x--0.5%29
Again, the answer is: 1, -0.5. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+2%2Ax%5E2%2B-1%2Ax%2B-1+%29

Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!

You don't need to use the quadratic formula,
as the other tutor used, because it leads to 
a factorable quadratic:

system%28xy=1%2C%0D%0A2x-y=1%29

Solve the second equation for y:

matrix%283%2C1%2C%0D%0A+++2x-y=1%2C%0D%0A+++2x-1=y%2C%0D%0A+++y=2x-1%0D%0A%29 

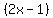Substitute %282x-1%29 in the first equation in the system



So there are two solutions for x.  We
must find a value of y for each of them,
by substituting each in y=2x-1

Substituting x=-1%2F2,
y=2x-1
y=2%28-1%2F2%29-1
y=-1-1
y=-2

So one solution is (x,y) = (-1%2F2,-2) 

Substituting x=1,
y=2x-1
y=2%281%29-1
y=2-1
y=1

So the other solution is (x,y) = (1,1)

---------------------------

Checking (x,y) = (-1%2F2,-2)

system%28xy=1%2C%0D%0A2x-y=1%29

system%28%28-1%2F2%29%28-2%29=1%2C%0D%0A2%28-1%2F2%29-%28-2%29=1%29

system%281=1%2C%0D%0A-1%2B2=1%29

system%281=1%2C%0D%0A1=1%29 

Checking (x,y) = (1,1)

system%28xy=1%2C%0D%0A2x-y=1%29

system%28%281%29%281%29=1%2C%0D%0A2%281%29-%281%29=1%29

system%281=1%2C%0D%0A2-1=1%29

system%281=1%2C%0D%0A1=1%29

Edwin