SOLUTION: Suppose line l contains the points (5, 6) and (4, 3). Determine the equation of the line that: (1) Has the same y-intercept as l (2) Is perpendicular to l.

The other tutor's solution is a different problem:

Here are those points plotted:



Now we get a ruler and draw a green line through them:



We find the equation of that green line that contains the points
(5, 6) and (4, 3) by using the slope formula



Now we use the point-slope form:





Now we simplify it to get the slope-y-intercept form





Comparing it to the slope-y-intercept form

, whose slope is m and whose y-intercept is (0,b)

We find that its y-intercept is (0,-9).

We can see in the graph above that the green line appears to 
have that y-intercept.

Now we want the equation of another line which is perpendicular
to that line.  It's slope will be the reciprocal of the slope 3
with the sign changed.  That is, the slope of the required line
will have slope .

This required line is to have the same y-intercept (0.-9), that
the given line has.

so its equation is



We already have one point on the required line, the y-intercept
(0,-9). We'll find another point on it, say, by substituting 






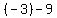
So we see that the required line goes through (-3,-8) and (0,-9)



Getting our ruler again, and drawing a blue line through (0,-9) and
(-3,-8) we have:



The blue line looks very much perpendicular to the green line
and so we are satisfied that 



is the required equation of the required line. 

If you like you can put it in general form by multiplying through by 3,
then adding x to both sides:



Edwin