SOLUTION: Find an equation of the line that contains the point (1,0) and is perpendicular to 2x+y=4.

Algebra ->  Linear-equations -> SOLUTION: Find an equation of the line that contains the point (1,0) and is perpendicular to 2x+y=4.      Log On


   

Question 262695: Find an equation of the line that contains the point (1,0) and is perpendicular to 2x+y=4.
Answer by PRMath(133) About Me  (Show Source):
You can put this solution on YOUR website!
Find an equation of the line that contains the point (1,0) and is perpendicular to 2x+y=4.

First you must know that lines perpendicular to on another have a slopes that are negative reciprocals of one another. For example, if a slope of a line is 4, a line perpendicular to that line will have a slope of %28-1%29%2F4. If you were to multiply 4%2F1 times %28-1%29%2F4 you would get -1. Negative reciprocals, when multiplied, will result in the number -1. :-)

If lines have the SAME slope, they are parallel.

Now that we have those facts, let's look at the line you are given. The equation for the line you are given is: 2x + y = 4. If you were to put this line into the slope intercept equation of a line, which is y = mx + b, then you'd see the slope immediately. In the equation y = mx + b, the slope is "m".

SO let's put your line into the y = mx + b format, which means that we will solve for y. Here goes:

2x + y = 4 (your original equation)
y = 4 - 2x (subtract 2x from both sides to isolate the y)

y = -2x + 4 (rewrite the equation so that the slope is clear to you)
y = mx + b

Looking above, can you see that m = -2? SO... if our slope is equal to -2, (which is the same as %28-2%29%2F1 the negative reciprocal to that number is going to be: 1%2F2. (I just flipped the fraction and changed the sign).

Our new line must have a slope of 1%2F2 and it must go thru point (1,0).

When we know a point on the line [in this case the point is (1,0)] and we know the slope, [in this case, we want a slope of 1%2F2]we should use the POINT SLOPE equation of a line, which is:

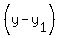%28y+-+y%5B1%5D%29 = m%28x+-+x%5B1%5D%29 Now that we know the formula, we just fill in the info we are given.

We want this: m = 1%2F2 thru point (1,0).
Let's plug that into the point slope equation of a line:


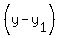%28y+-+y%5B1%5D%29 = m%28x+-+x%5B1%5D%29 (point slope equation of a line)
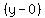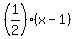%28y+-+0%29 = %281%2F2%29%28x+-+1%29 (point slope equation with slope of 1%2F2 and point (1,0) plugged in)
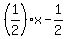y = %281%2F2%29x+-+1%2F2 (distributed 1%2F2 to the x and distributed 1%2F2 to the %28-1%29.

Now we have our equation of a line that is perpendicular to the first equation you were given. y = 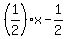%281%2F2%29x+-+1%2F2

I hope this helps you. :-)