|
Question 252412: I have been sitting here for hours trying to figure the following problems. I am working on Non-Linear Systems and have to solve the following systems. No matter how I work it I can't seem to come to a solution.
1) {7x-8y=24
{xy^2=1
2) {(x+1)^2 - (y-1)^2 = 20
{x^2 - (y+2)^2 - 24
Thank you - Lori
Found 2 solutions by jim_thompson5910, Edwin McCravy:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
Answer by Edwin McCravy(20066)   (Show Source): (Show Source):
You can put this solution on YOUR website!
1)
 solve the first equation for y:
solve the first equation for y:


 Substitute in the second equation:
Substitute in the second equation:

 Multiply both sides by 64
Multiply both sides by 64
 Square the binomial:
Square the binomial:

 Possible rational zeros of that are
± fractions whose numerators are
factors of 64 and whose denominators
are factors of 49.
The factors of 64 are 1,2,4,8,16,32,64
The factors of 49 are 1,7,49
We try the easiest one first in hopes
the person who made up this problem
was kind.
We try x=1, so we divide by x-1
1 | 49 -336 576 -64
| 49 -287 289
------------------
49 -287 289 225
Doesn't leave a 0 remainder.
We try x=2, so we divide by x-2
2 | 49 -336 576 -64
| 98 -476 200
------------------
49 -238 100 136
Doesn't leave a 0 remainder.
We try x=4, so we divide by x-4
4 | 49 -336 576 -64
| 196 -560 64
------------------
49 -140 16 0
Hooray! It leaves a 0 remainder!
So we have factored the left side of
the equation
Possible rational zeros of that are
± fractions whose numerators are
factors of 64 and whose denominators
are factors of 49.
The factors of 64 are 1,2,4,8,16,32,64
The factors of 49 are 1,7,49
We try the easiest one first in hopes
the person who made up this problem
was kind.
We try x=1, so we divide by x-1
1 | 49 -336 576 -64
| 49 -287 289
------------------
49 -287 289 225
Doesn't leave a 0 remainder.
We try x=2, so we divide by x-2
2 | 49 -336 576 -64
| 98 -476 200
------------------
49 -238 100 136
Doesn't leave a 0 remainder.
We try x=4, so we divide by x-4
4 | 49 -336 576 -64
| 196 -560 64
------------------
49 -140 16 0
Hooray! It leaves a 0 remainder!
So we have factored the left side of
the equation
 as
as
 So we use the zero factor property
So we use the zero factor property
 which gives the value which gives the value 
 That does not factor, so we have to use the quadratic
formula:
That does not factor, so we have to use the quadratic
formula:





 Now we must substitute each of the 3 values for x
into
Now we must substitute each of the 3 values for x
into
 Substituting
Substituting 




 Therefore on soluton is (4,
Therefore on soluton is (4, )
-----
Substituting )
-----
Substituting 

 Divide through by 2
Divide through by 2
 Divide both sides by 4
Divide both sides by 4
 So another solution is
(x,y) = (
So another solution is
(x,y) = (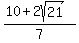 , , )
---
Substituting )
---
Substituting 

 Divide through by 2
Divide through by 2
 Divide both sides by 4
Divide both sides by 4
 So another solution is
(x,y) = (
So another solution is
(x,y) = (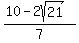 , ,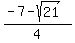 )
---
2) {(x+1)^2 - (y-1)^2 = 20
{x^2 - (y+2)^2 - 24
Sorry, but you left out the equal sign in the second
Re-post it corrected and we can help you. There must be
an equal sign somewhere in that. You probably meant for
one of the - signs to be an = sign but we can't tell
which one.
Edwin )
---
2) {(x+1)^2 - (y-1)^2 = 20
{x^2 - (y+2)^2 - 24
Sorry, but you left out the equal sign in the second
Re-post it corrected and we can help you. There must be
an equal sign somewhere in that. You probably meant for
one of the - signs to be an = sign but we can't tell
which one.
Edwin
|
|
|
| |