Question 231910: Solve for the following items:
a. The point on the x-axis that is equidistant (equal distance) from (12,6) and (8,2).
b. The distance between the points (6,4) and (18,4).
c. The distance between the points (1,4) and (19,6).
d. The midpoint between (12, 6) and (18, 4)
e. The midpoint between (-6, -8) and (23, 5)
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! One can find the distance between two points, from the coordinates of those points, using the distance formula:

We will use this formula for each of the first three problems. We will use the midpoint formula for the midpoint problems:


a) The point on the x-axis that is equidistant (equal distance) from (12,6) and (8,2)
Since all points on the x-axis have a y-coordinate that is zero, we are going to use (x, 0) for the coordinates of the point we are seeking. We can use the distance formula to express the distance between this point and (12, 6):

... and the distance between this point and (8, 2):

Since (x, 0) is supposed to be equidistant from the other two, the two distances we have expressed must be equal (i.e.  ): ):

We can use this equation to solve for x. We'll start by simplifying both sides:



Now we'll square both sides to eliminate the square roots:

Subtract  from each side: from each side:

Add 24x to both sides:

Subtract 68 from each side:

Divide both sides by 8:

So the solution is: (14, 0)
b. The distance between the points (6,4) and (18,4).




c. The distance between the points (1,4) and (19,6).




which will simplify:

d. The midpoint between (12, 6) and (18, 4)
Midpoint: (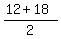 , ,  ) )
Midpoint: ( , ,  ) )
Midpoint: ( , ,  ) )
e. The midpoint between (-6, -8) and (23, 5)
Midpoint: ( , , 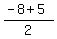 ) )
Midpoint: ( , ,  ) )
Midpoint: (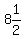 , , 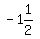 ) )
|
|
|