SOLUTION: write an equation for each line, then graph the line. through (-1,3) and parallel to y=2x+1 through (2,2) and perpendicular to y=-3/5x+2 through (-3,4) and vertical thr

(1). The equation of a non-vertical graphed line that goes through point
(x1,y1) and has slope  is

(2). 

(3). The equation of a non-vertical graphed line that has slope  and 
y-intercept 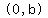 is 



(4). Two non-vertical parallel lines have the same slope.

(5). Two non-vertical perpendicular lines have slopes one of which
is the reciprocal of the other with the sign changed.

(6). A vertical line has no slope and has the equation  where
 represents its distance from the y-axis, right of the y-axis
if  is positive and left of the y-axis if  is negative.
 is the equation of the vertical line that coincides with
the y-axis.

(7). A horizontal line has slope .

-----------------------------

through (-1,3) and parallel to 

We draw the line  by plotting a couple of points
and draw it in light green:



Next we plot the point (-1,3)



And we draw a black line through that point 
parallel to the green line:



That black line is the line we need the equation for.

So, from  we use (3) above to find that 

From (4) we know that we will use the same slope .

Next we use (1) to find the equation:

 where (x1,y1) = (-1,3)
and 


 






-------------------------

We draw the line  by plotting a couple of points
and draw it in light green:



Next we plot the point (2,2)



And we draw a black line through that point 
perpendicular to the green line:



That black line is the line we need the equation for.

So, from  we use (3) above to find that 

From (5) we know that we will use the slope which is found
by inverting 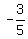 and changing its sign, and so we
use  for the black line.

Next we use (1) to find the equation:

 where (x1,y1) = (2,2)
and 


 











-------------------------

We plot the point:



and draw a vertical line through it:



Now we use (6) above and realize that the vertical line is 3
units to the left of the the y-axis and thuse its equation
is 

--------------------------------

We plot the point:



and draw a horizontal line through it:



Now we use (7) above which tells us the slope 

Next we use (1) to find the equation:

 where (x1,y1) = (4,1)
and 


 





--------------------------------
Edwin