|
Question 205592: Point A (-4,1) is in the standard (x,y) coordinate plane. What must be the coordinates of point B so that the line x=2 is the perpendicular bisector of AB? (with a line above the AB - what does that mean?) The answer is (8,1). How was this answer determined?
This is a sample question from a review of questions that I might have on a placement test to determine my math knowledge. I am going back to college for more eduation after many years away from it.
Thank you!
Found 2 solutions by stanbon, Earlsdon:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Point A (-4,1) is in the standard (x,y) coordinate plane. What must be the coordinates of point B so that the line x=2 is the perpendicular bisector of AB? (with a line above the AB - what does that mean?) The answer is (8,1). How was this answer determined?
------------------------------------
Draw a coordinate system.
plot the point A(-4,-1)
Draw the verticle line x=2
-------------------
Notice that A is 6 to the left of x=2.
Therefore B must be 6 to the right of x=2
B is on the same y-level as A
So B = (2+6,-1) or (8,-1)
===============================
Cheers,
Stan H.
Answer by Earlsdon(6294)   (Show Source): (Show Source):
You can put this solution on YOUR website! First, AB with a line above it is shorthand for "line segment AB".
Given point A is (-4, 1).
Now since the line segment AB is bisected by the perpendicular line x = 2, (a vertical line) then you can conclude that the midpoint of line segment AB is at the point (2, 1).
Why, because the line segment AB is horizontal and we know this because the line x = 2 (a vertical line) is the perpendicular bisector of line segment AB, and the line x = 2 must pass through the center of the line segment AB and intersect it at the point (2, 1).
So, using the midpoint formula which gives us the x- and y-coordinates of the midpoint (2, 1):
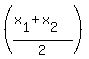 , ,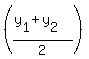 where: where:  and and  substituting, we get: substituting, we get:
 and... and...
 we can solve for we can solve for  and and  which will be the x- and y-coordinates of point B. which will be the x- and y-coordinates of point B.
 Multiply both sides by 2. Multiply both sides by 2.
 Now add 4 to both sides. Now add 4 to both sides.
 and for the y-coordinate of B... and for the y-coordinate of B...
 Multiply both sides by 2. Multiply both sides by 2.
 Subtract 1 from both sides. Subtract 1 from both sides.

The coordinates of point B are (8, 1)
|
|
|
| |