SOLUTION: Can you explain how to graph linear equations, for ex. y = 2x, y = 5-x and 4x + 6y = 8

Algebra ->  Linear-equations -> SOLUTION: Can you explain how to graph linear equations, for ex. y = 2x, y = 5-x and 4x + 6y = 8      Log On


   

Question 166674This question is from textbook
: Can you explain how to graph linear equations, for ex. y = 2x, y = 5-x and 4x + 6y = 8 This question is from textbook

Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
# 1


Let's graph y=2x


Looking at y=2x we can see that the equation is in slope-intercept form y=mx%2Bb where the slope is m=2 and the y-intercept is b=0 note: y=2x really looks like y=2x%2B0


Since b=0 this tells us that the y-intercept is .Remember the y-intercept is the point where the graph intersects with the y-axis

So we have one point




Now since the slope is comprised of the "rise" over the "run" this means
slope=rise%2Frun

Also, because the slope is 2, this means:

rise%2Frun=2%2F1


which shows us that the rise is 2 and the run is 1. This means that to go from point to point, we can go up 2 and over 1



So starting at , go up 2 units


and to the right 1 unit to get to the next point



Now draw a line through these points to graph y=2x

So this is the graph of y=2x through the points and






# 2

Let's graph y=5-x


First rearrange the terms to get y=-x%2B5


Looking at y=-x%2B5 we can see that the equation is in slope-intercept form y=mx%2Bb where the slope is m=-1 and the y-intercept is b=5


Since b=5 this tells us that the y-intercept is .Remember the y-intercept is the point where the graph intersects with the y-axis

So we have one point




Now since the slope is comprised of the "rise" over the "run" this means
slope=rise%2Frun

Also, because the slope is -1, this means:

rise%2Frun=-1%2F1


which shows us that the rise is -1 and the run is 1. This means that to go from point to point, we can go down 1 and over 1



So starting at , go down 1 unit


and to the right 1 unit to get to the next point



Now draw a line through these points to graph y=-x%2B5

So this is the graph of y=-x%2B5 through the points and






# 3


In order to graph ANY linear equation, you MUST solve for "y" first.


4x%2B6y=8 Start with the given equation.


6y=8-4x Subtract 4x from both sides.


6y=-4x%2B8 Rearrange the terms.


y=%28-4x%2B8%29%2F%286%29 Divide both sides by 6 to isolate y.


y=%28%28-4%29%2F%286%29%29x%2B%288%29%2F%286%29 Break up the fraction.


y=-%282%2F3%29x%2B4%2F3 Reduce.


Now let's graph y=-%282%2F3%29x%2B4%2F3




In order to graph this equation, we only need two points to create a straight line




----------------Let's find the first point----------------------


y=-%282%2F3%29x%2B4%2F3 Start with the given equation


y=-%282%2F3%29%282%29%2B4%2F3 Plug in x=2


y=-4%2F3%2B4%2F3 Multiply -2%2F3 and 2 to get -4%2F3


y=0%2F3 Add the fractions


y=0 Reduce



So when x=2, we have the value y=0. This means we have the first point




----------------Let's find the first point----------------------


y=-%282%2F3%29x%2B4%2F3 Start with the given equation


y=-%282%2F3%29%285%29%2B4%2F3 Plug in x=5


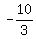
y=-10%2F3%2B4%2F3 Multiply -2%2F3 and 5 to get -10%2F3


y=-6%2F3 Add


y=-2 Reduce



So when x=5, we have the value y=-2. This means we have the second point




------------------------------------------------------------------------------------------------


So we have the two points: and


Now plot these two points on a coordinate system





Now draw a straight line through the two points. This line is the graph of y=-%282%2F3%29x%2B4%2F3

Graph of y=-%282%2F3%29x%2B4%2F3 through the two points and