Question 155038: for what value(s) of p does the equation x^2+px+1=0 have no real solutions, and two real solutions.
Answer by Fombitz(32388)   (Show Source): (Show Source):
You can put this solution on YOUR website! For this discussion, we'll use the discriminant.
For the general quadratic equation,

the discriminant is

.
.
If  then you have two distinct real roots. then you have two distinct real roots.
If  , you have a double root, one real root occurring twice , you have a double root, one real root occurring twice
If 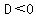 , you have two complex roots, that are complex conjugates. , you have two complex roots, that are complex conjugates.



For no real (complex) solutions,
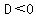


Valid interval: (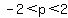 ) )
.
.
.
.
For two real solutions,


 and and 
Valid interval:( , , ]U[ ]U[ , , ) )
|
|
|