SOLUTION: sketch the parabola {{{ y = x^2-7x+12 }}} using the algorithm. Label axis of symetry, vertex, and x and y intercepts

Algebra ->  Linear-equations -> SOLUTION: sketch the parabola {{{ y = x^2-7x+12 }}} using the algorithm. Label axis of symetry, vertex, and x and y intercepts      Log On


   

Question 153203: sketch the parabola +y+=+x%5E2-7x%2B12+ using the algorithm. Label axis of symetry, vertex, and x and y intercepts
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
Vertex:


In order to find the vertex, we first need to find the x-coordinate of the vertex.


To find the x-coordinate of the vertex, use this formula: x=%28-b%29%2F%282a%29.


x=%28-b%29%2F%282a%29 Start with the given formula.


From y=x%5E2-7x%2B12, we can see that a=1, b=-7, and c=12.


x=%28-%28-7%29%29%2F%282%281%29%29 Plug in a=1 and b=-7.


x=%287%29%2F%282%281%29%29 Negate -7 to get 7.


x=%287%29%2F%282%29 Multiply 2 and 1 to get 2.


So the x-coordinate of the vertex is x=7%2F2. Note: this means that the axis of symmetry is also x=7%2F2.


Now that we know the x-coordinate of the vertex, we can use it to find the y-coordinate of the vertex.


y=x%5E2-7x%2B12 Start with the given equation.


y=%287%2F2%29%5E2-7%287%2F2%29%2B12 Plug in x=7%2F2.


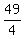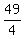y=1%2849%2F4%29-7%287%2F2%29%2B12 Square 7%2F2 to get 49%2F4.


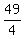y=49%2F4-7%287%2F2%29%2B12 Multiply 1 and 49%2F4 to get 49%2F4.


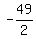y=49%2F4-49%2F2%2B12 Multiply -7 and 7%2F2 to get -49%2F2.


y=-1%2F4 Combine like terms.


So the y-coordinate of the vertex is y=-1%2F4.


So the vertex is which in decimal form is (3.5, -0.25).


------------------------------------------


x-intercept(s):


y=x%5E2-7x%2B12 Start with the given equation.


0=x%5E2-7x%2B12 Plug in y=0



x%5E2-7x%2B12=0 Start with the given equation


%28x-4%29%28x-3%29=0 Factor the left side (note: if you need help with factoring, check out this solver)



Now set each factor equal to zero:
x-4=0 or x-3=0

x=4 or x=3 Now solve for x in each case


So the answers are

x=4 or x=3


which means that the x-intercepts are (4,0) and (3,0)


--------------------------------------

y-intercept:


y=x%5E2-7x%2B12 Start with the given equation.


y=%280%29%5E2-7%280%29%2B12 Plug in x=0


y=12 Simplify


So the y-intercept is (0,12)



So with all of this info, we get this sketch:

Graph of y=x%5E2-7x%2B12


note: the point (7,12) is a reflection of the point (0,12)