SOLUTION: Line l goes throught the point (5,–2) and is perpendicular to the line through (–2, 1) and (–4, –2). Find the equation (in slope-intercept form) for l.

Algebra ->  Linear-equations -> SOLUTION: Line l goes throught the point (5,–2) and is perpendicular to the line through (–2, 1) and (–4, –2). Find the equation (in slope-intercept form) for l.       Log On


   

Question 150620: Line l goes throught the point (5,–2) and is perpendicular to the line through (–2, 1) and (–4, –2). Find the equation (in slope-intercept form) for l.
Answer by Earlsdon(6294) About Me  (Show Source):
You can put this solution on YOUR website!
The equation you want will look like:
y+=+mx%2Bb
Let's first find the slope, m.
Since the slope of the line you want is perpendicular to the line through the two points (-2, 1) and (-4, -2), and you know that perpendicular lines have slopes that are the negative reciprocal of each other, then once you have the slope of the line through the two given points, you will have the slope of your line.
The slope of the line through the two given points is:
m+=+%28y%5B2%5D-y%5B1%5D%29%2F%28x%5B2%5D-x%5B1%5D%29 Make the appropriate substitutions of the x's and y's from the two given points:
m+=+%28-2-1%29%2F%28-4-%28-2%29%29 Simplify this.
m+=+-3%2F-2
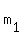m+=+3%2F2 The slope m%5B1%5D of your line will be the negative reciprocal of this, so,...
m%5B1%5D+=+%28-2%2F3%29
Now you can write the starting equation for your line:
y+=+%28-2%2F3%29x+%2B+b Next, you need to find the value of b, the y-intercept.
You can do this by subtituting the x- and y-cordinates of the point (5, -2) through which your line passes.
-2+=+%28-2%2F3%295+%2B+b Simplify and solve for b.
-2+=+%28-10%2F3%29%2Bb Add 10%2F3 to both sides and convert -2+=+-6%2F3.
-6%2F3%2B10%2F3+=+b Simplify.
b+=+4%2F3
So your final equation, in slope-intercept form is:
y+=+%28-2%2F3%29x%2B4%2F3