SOLUTION: determine from the slopes and y-intercepts of the two lines wether the linearequations that name those lines are -inconsistent,consistent or dependent. If the equations are consis

Algebra ->  Linear-equations -> SOLUTION: determine from the slopes and y-intercepts of the two lines wether the linearequations that name those lines are -inconsistent,consistent or dependent. If the equations are consis      Log On


   

Question 149382: determine from the slopes and y-intercepts of the two lines wether the linearequations that name those lines are -inconsistent,consistent or dependent. If the equations are consistent,find the common solutionof that system of equations. A. y=5x+3 5x-y=7 __________ . B. x-3y=13 3x=9y+39 _________ . C. 3x-2y=5 2y=3x+7 __________ . D. x+4/5y=4 x-1/2y=-9 ________ .would someone help?
Answer by Earlsdon(6294) About Me  (Show Source):
You can put this solution on YOUR website!
Since you have to find the same things for all four of your problems, I'll do one of them and you can use this response as a guide for doing the others.
If you still have difficulty then re-post.
The equations with fractions are usually most troublsome for students, so I'll go through problem D.
D.
1) x%2B%284%2F5%29y+=+4
2) x-%281%2F2%29y+=+-9
First, we'll find the slopes. To do this, you need to rearrange your equations so thet they in the "slope-intercept" form: y+=+mx%2Bb
1) x%2B%284%2F5%29y+=+4 Multiply both sides by 5 to clear the fraction.
5%28x%2B%284%2F5%29y%29+=+5%284%29 Simplify.
5x%2B4y+=+20 Now you need to get the y on one side of the = sign and everythng else on the other side. Subtact 5x from both sides.
5x-5x%2B4y+=+-5x%2B20
4y+=+-5x%2B20 Now you divide both sides by 4 to get the y by itself.
4y%2F4+=+%28-5x%2B20%29%2F4 Simplify.
y+=+%28-5%2F4%29x%2B5 Now compare this with the "slope-intercept" form:
y+=+mx%2Bb You can see that the slope, highlight%28m+=+%28-5%2F4%29%29 and that the y-intercept, highlight%28b+=+5%29
2) x-%281%2F2%29y+=+-9 Multiply both sides by 2 to clear the fraction.
2%28x-%281%2F2%29y%29+=+2%28-9%29 Simplify.
2x-y+=+-18 Now add y to both sides of the equation.
2x-y%2By+=+y-18 Simplify.
2x+=+y-18 Next, add 18 to both sides.
2x%2B18+=+y-18%2B18 Simplify.
2x%2B18+=+y We usully want to see the y on the left side, so...
y+=+2x%2B18 Now compare this with the "slope-intercept" form:
y+=+mx%2Bb You can see that highlight%28m+=+2%29 and that the y-intercept highlight%28b+=+18%29
Now let's find the solution to this system of equations:
We have already converted the equations to their corresponding slope-intercept forms, so we'll start there:
y%5B1%5D+=+%28-5%2F4%29x%2B5
y%5B2%5D+=+2x%2B18
Now, since both of these equations are equal to y, we can set them equal to each other and solve for x.
%28-5%2F4%29x%2B5+=+2x%2B18 Multiply both sides by 4 to clear the fraction.
-5x%2B20+=+8x%2B72 Add 5x to both sides.
20+=+13x%2B72 Subtract 72 from both sides.
-52+=+13x Divide both sides by 13.
-4+=+x or highlight%28x+=+-4%29 Now substitute this value of x into either one of the two equations we started with to solve for y.
Let's use y%5B2%5D+=+2x%2B18 Substitute x = -4
y+=+2%28-4%29%2B18 Simplify.
y+=+-8%2B18
highlight%28y+=+10%29
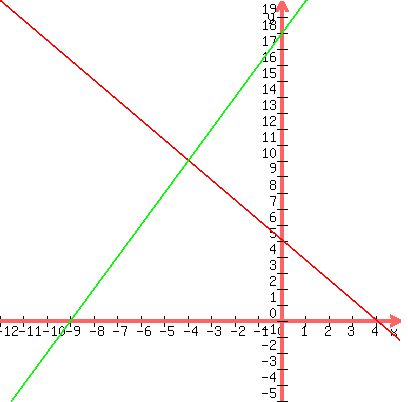
The solution is (-4, 10)
There is exactly one solution to this system of equations so the system is "consistent" and "independent"
Let's look at the graph:
graph%28400%2C400%2C-12%2C5%2C-5%2C20%2C%28-5%2F4%29x%2B5%2C2x%2B18%29