|
Question 149043: I need to write this problem into slope-intercept form and i don't know how.
passing though (3,6) and (2, -6)
Found 2 solutions by mangopeeler07, Earlsdon:
Answer by mangopeeler07(462)   (Show Source):
You can put this solution on YOUR website! slope-intercept form: y=mx+b
First solve for m, the slope:
difference of y's over difference of x's [(3,6) and (2, -6)]
6--6/3-2
Simplify
12/1
Slope=m=12
y=12x+b
plug in coordinates (either pair)
6=12(3)+b
Simplify
6=36+b
Subtract 36
-30=b
y=mx+b (don't plug in coordinates now, just m and b)
y=12x+-30
y=12x-30
Answer by Earlsdon(6294) (Show Source):
You can put this solution on YOUR website! Start with the general slope-intercept form of a linear equation:
y = mx+b where m is the slope and b is the y-intercept.
Then find the slope of the line that passes through the points (3, 6) and (2, -6), using the formula:
In this problem, ( , ) = (3, 6) and ( , ) = (2, -6)
Making the apprpropriate substitutions, you get:
 Simplifying...
So now you can write:
 but now you need to find the value of b and you can do this by substiting the x- and y-coordinates of either one of the two given points.
Let's use the first point (3, 6) and substitute x = 3 and y = 6 into the above equation.
 Simplify and solve for b.
 Subtract 36 from both sides.
Now you can write the final equation because you have m = 12 and b = -30
Let's see what the graph of this equation looks like:
|
|
|
| |
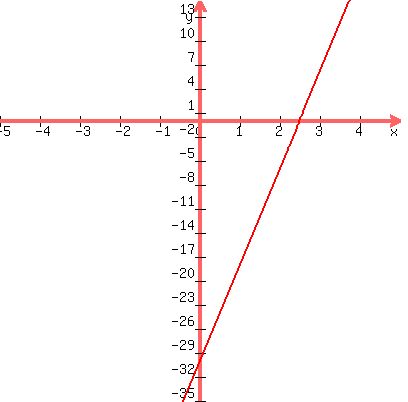
