|
Question 136149: Is a person's age a function of his or her height? Explain. THANKS!
Found 2 solutions by MathLover1, solver91311:
Answer by MathLover1(20854)   (Show Source):
Answer by solver91311(24713)  (Show Source):
You can put this solution on YOUR website! A function is a relationship between some variable or variables and the value of the function with the very important restriction that any given value of the independent variable(s) may map to one and only one value of the function. Note that it is perfectly ok if more than one value of the independent variable maps to the same function value.
So, the answer to your question is: It depends. The wording of your question has height as the independent variable and age as the value of the function.
If age has the traditional meaning of "the positive integer number of anniversaries of a person's birth that have occured" and height has the typical precision to the nearest inch or centimeter, then 5'6" tall certainly maps to several different ages. All you would have to do would be to find a 5'6" 20 year old and a 5'6" 40 year old to prove the fact that the relation is not a function. From this point of view, the answer is no.
On the other hand, if you were to measure height with sufficient precision, it is theoretically possible that no two people on earth have the exact same height (if you do find two people with the same height at the level of precision you are using, just increase the level of precision until they are different). Of course, you would certainly be measuring height down to some fraction of an Angstrom (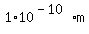 ), but that would mean that every person on earth has a unique height, and that height would map to one and only one age, namely that person's age. In this case, age would be a function of height. It wouldn't be a very useful function, because there is no mathematical rule to define it, but it would be a function nonetheless.
|
|
|
| |
