|
Question 126664: I have a 2 questions, they are comfusing me, Laura and Brent paddled a canoe 6 miles upstream in four hours. The return trip took 3 hours. Find the rate at which Laura and Brent paddled the canoe in still water......that is one, and the other is, The sum of the digits of a 2-digit # is 11. If the digits are reversed, the new number is 45 more than the original numer. Find the number
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! You know that distance = rate X time or  , or, since we are trying to determine a rate: , or, since we are trying to determine a rate:  . .
For both the upstream and downstream trips we know the distance is 6 miles and the times, 4 hours and 3 hours respectively.
For the upstream trip, the true rate of speed of the boat is the boat's rate of speed in still water MINUS the rate of the current. For the downstream trip, the true rate is the still water rate PLUS the rate of the current.
Upstream equation:  , where , where 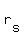 is the rate in still water and is the rate in still water and 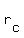 is the rate of the current. is the rate of the current.
Downstream equation: 


Now add the equations, term-by-term:

And solve:


So the rate in still water is  mph. mph.
Check:
To go 6 miles in 4 hours, the true rate must have been  mph. To go 6 miles in 3 hours, the true rate must have been mph. To go 6 miles in 3 hours, the true rate must have been  mph. mph.
 means that means that  . .  , answer checks. , answer checks.
================================================================
Let the 10s digit be x and the 1s digit be y. The sum of the digits is 11, so:

And the original number is n, where 
If you reverse the digits, the new number which is 45 more than the old number would be given by:
 , but this can be written: , but this can be written:  . .
Now we have two expressions that are equal to n, so we can set these two expressions equal to each other:




From our first equation:  , we can get , we can get  and we can substitute this expression for y into the previous result: and we can substitute this expression for y into the previous result:





Now substituting this value for x into the first equation:


So the original number is 38.
Check:
3 + 8 = 11.
83 - 38 = 45. Answer checks.
|
|
|
| |