|
Question 123193: Hi May I have some help solving this problem?
Find a point on the y-axis that is equidistant from the points (8, -8) and (2, 2).
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find a point on the y-axis that is equidistant from the points (8, -8) and (2, 2).
:
Since the point is on the y axis we know the x coordinate = 0
Call the point: 0,y and solve for y
:
Use the distance formula d = 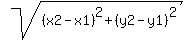
:
In the distance equation let x1 = 0 and y1 = y
:
dist from points 2,2 to 0,y = dist from points 8,-8 to 0,y
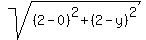 = = 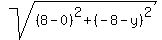
Square both sides and we can forget about the radicals
:
4 + (4 - 4y + y^2) = 64 + (64 + 16y + y^2)
:
8 - 4y + y^2 = 128 + 16y + y^2
:
Group the y's on the left and numerical values on the right
y^2 - y^2 - 4y - 16y = 128 - 8
:
Conveniently the y^2 cancel so we have:
-20y = 120
:
Divide both sides by -20
y = 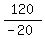
y = -6
:
Equidistant point on the y axis = 0,-6
:
:
Rather than check our solution in the distance equations, I plotted these
points on piece of graph paper and, it indeed checks out! You can do the same.
:
Hope I made this understandable. Any questions?
|
|
|
| |