|
Question 1209272: Write an equation of the line in slope-intercept form.
A line graphed on a coordinate plane. The x-axis ranges from negative 3 to 5, in increments of 1. The y-axis ranges from negative 1 to 7, in increments of 1. The line passes through the points at ordered pair 0 comma 5 and ordered pair 3 comma 4.
An equation is:
Found 3 solutions by josgarithmetic, MathTherapy, greenestamps:
Answer by josgarithmetic(39630)   (Show Source): (Show Source):
Answer by MathTherapy(10557)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Write an equation of the line in slope-intercept form.
A line graphed on a coordinate plane. The x-axis ranges from negative 3 to 5, in increments of 1. The y-axis ranges from negative 1 to 7, in increments of 1. The line passes through the points at ordered pair 0 comma 5 and ordered pair 3 comma 4.
An equation is:
He's WRONG. The slope is NOT - 1, as 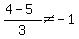 .
Ordered pair: (0, 5) and (3, 4), so m, or slope = .
Ordered pair: (0, 5) and (3, 4), so m, or slope = 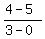 = = 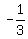 .
Since the y-intercept was given as point (0, 5), we get the CORRECT equation as: .
Since the y-intercept was given as point (0, 5), we get the CORRECT equation as:  .
In order for the graph to show the line, the y-axis can range from - 1 to 7, but the x-axis NEEDS to range
from - 3 to 15, i/o from - 3 to 5, in order for the equation: .
In order for the graph to show the line, the y-axis can range from - 1 to 7, but the x-axis NEEDS to range
from - 3 to 15, i/o from - 3 to 5, in order for the equation:  to be clearly viewed. to be clearly viewed.

Answer by greenestamps(13216)   (Show Source): (Show Source):
You can put this solution on YOUR website!
One of the given points, (0,5), is the y-intercept, so the equation in slope-intercept form is of the form y=mx+5.
Use the coordinates of the other given point to determine the slope m to complete the equation.
You can plug numbers into the equation for calculating the slope. But I think it gives the student a better understanding if you simply use the "rise over run" definition of slope.
From (0,5) to (3,4), you move (3-0) = 3 units in the x direction ("run") and (4-5) = -1 in the y direction ("rise"), so the slope "rise over run" is -1/3.
And then the equation in slope-intercept form of the line through the two given points is
ANSWER: y = (-1/3)x+5
|
|
|
| |