SOLUTION: The equation 5/(x + 3) + 3 = (8 + x)/(x + 3) has no solution, yet when we go through the process of solving it we obtain x = -3. Why is that the case?

Algebra ->  Linear-equations -> SOLUTION: The equation 5/(x + 3) + 3 = (8 + x)/(x + 3) has no solution, yet when we go through the process of solving it we obtain x = -3. Why is that the case?       Log On


   

Question 1207383: The equation 5/(x + 3) + 3 = (8 + x)/(x + 3) has no solution, yet when we go through the process of solving it we obtain x = -3. Why is that the case?
Found 3 solutions by Theo, greenestamps, ikleyn:
Answer by Theo(13342) About Me  (Show Source):
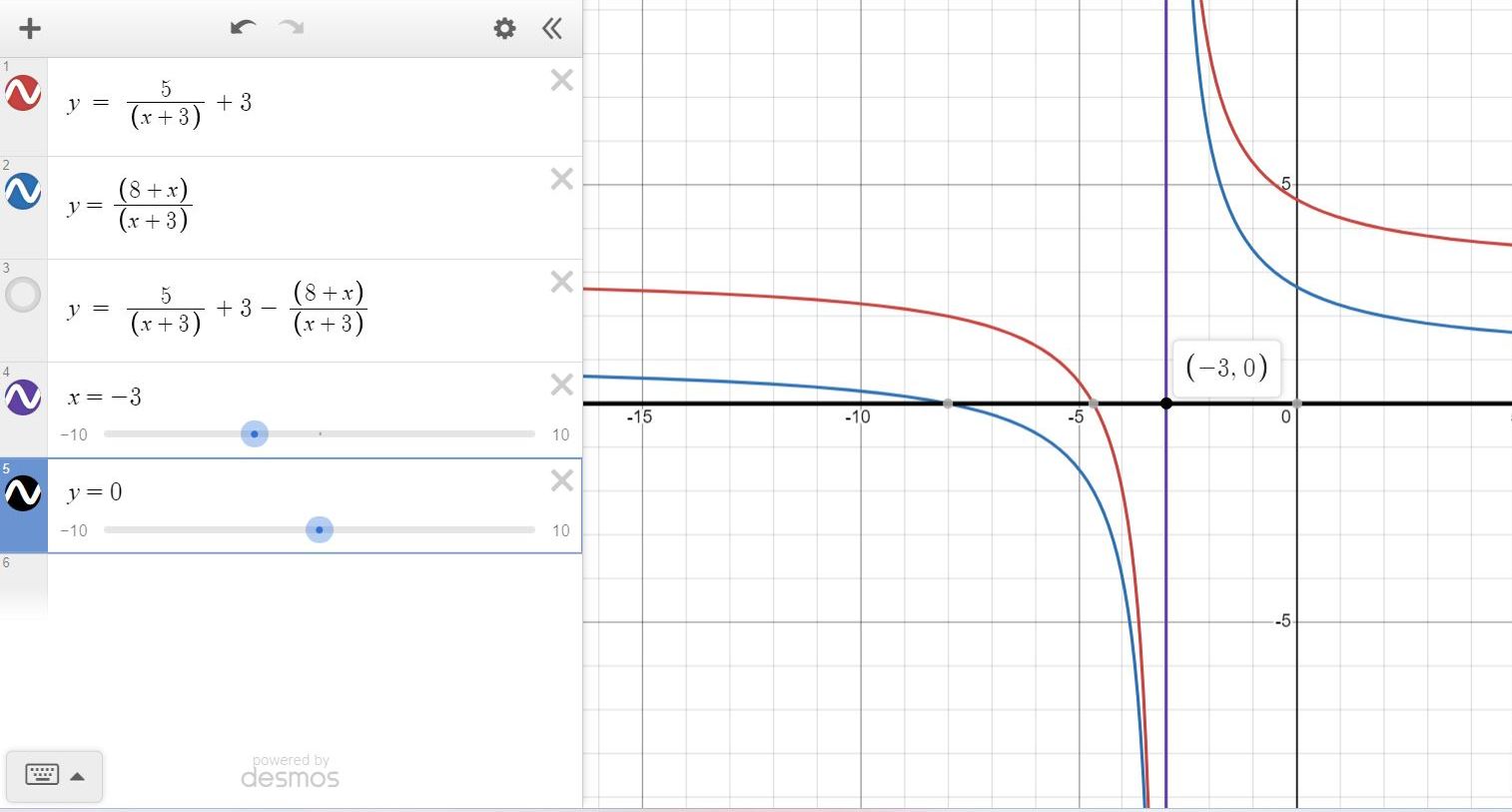
You can put this solution on YOUR website!
i graphed the equation and it looks like you have a vertical asymptote at x = -3.

if so, it means that x approaches -3 but never touches it.

i don't believe you will actually be able to solve the original equation at x = -3.

the value of y at x = -3 should be undefined.

since your equation is y = 5/(x+3, the value of y is undefined at x = -3 because the divisor becomes 0.

same for (8+x)/(x+3)

if you multiply both sides of the equation by (x+3), you eliminate the division by 0 as a possible solution, but that isn't the original equation.

the graph clearly shows that there is a vertical asymptote at x = -3.

if you do the calculations on the origiinal expressions on each side of the equation, you will see that y gets more positive as x approaches -3, or more negative as x approaches -3 from the other direction, but you can never get x = -3 as a possible soluton because of the division by 0.

here's my graph.



here's a reference on asymptotes.

https://www.mathsisfun.com/algebra/asymptote.html

the key to finding the asymptotes is that you have to look at the original equation.

if you change the equation by multiplying both sides by the denominator, you lose sight of the fact that there are vertical asymptotes.

i think that's what you did when you multiplied both sides of the equation by (x+3).

using graphing software helps you to see the equation to determine if any of those asymptotes exist.

the reference i gave you discusses ways to determine them, i believe.

the graphing software i used is at https://www.desmos.com/calculator

here's another reference on asymptotes that may be more informative.

https://www.andrews.edu/~rwright/Precalculus-RLW/Text/02-07.html#:~:text=To%20find%20the%20vertical%20asymptotes,zero%20and%20solve%20for%20x.&text=This%20is%20already%20factored%2C%20so,factor%20to%20zero%20and%20solve.&text=Since%20the%20asymptotes%20are%20lines,%3D%203%20and%20x%20%3D%201.



Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


If you get the answer x = -3 when you "go through the process of solving" the equation, then your process is flawed.

5%2F%28x%2B3%29%2B3=%288%2Bx%29%2F%28x%2B3%29

5%2F%28x%2B3%29%2B%283%28x%2B3%29%29%2F%28x%2B3%29=%288%2Bx%29%2F%28x%2B3%29

%285%2B3x%2B9%29%2F%28x%2B3%29=%288%2Bx%29%2F%28x%2B3%29

%283x%2B14%29%2F%28x%2B3%29=%288%2Bx%29%2F%28x%2B3%29

The denominators are the same, so the numerators must be equal:

3x%2B14=8%2Bx
2x=-6
x=-3

The solution, IF THERE IS ONE, is x = -3. But that "solution" is subject to the restriction that the denominator can't be zero.

When x = -3, the denominator IS zero. So the only POTENTIAL solution is not a solution; the equation has no solution.

ANSWER: no solution

Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.

The value  x = -3  is  PROXIBITED  for this equation,
since the fractions in both sides of this equations are not defined at  x = -3.

As people say in  Math,  the value  x = -3  is not in the domain of this equation,
while we are looking for the solutions that  ARE  in the domain.

When we get the solution  x = -3,  we get it for  ANOTHER,  transformed equation,
and this value does not work for the original equation.

The original equation and the transformed equation are NOT equivalent.


This is a complete explanation, in few words.   Full and complete.