|
Question 1207048: A farmer has just bought a new tractor for NAD800 000. He has to replace the
tractor in 5 years’ time, when its trade-in value will be NAD200 000. The
replacement cost of the tractor is expected to increase by 8% per annum.
2. The farmer wants to replace his present tractor with a new one in 5 years’ time.
The farmer wants to pay cash for the new tractor, after trading in his present
tractor for NAD200 000. How much will he need to pay?
(5 MARKS)
3. One month after purchasing his present tractor, the farmer deposited x NAD
into an account that pays interest at the rate of 12% p.a compounded monthly.
He continued to deposit the same amount at the end of each month for a total
of 60 months. At the end of 60 months, he has exactly the amount that is needed
to purchase a new tractor, after he trades in his present tractor. Calculates the
value of x.
(5 MARKS)
4. Suppose that 12 months after the purchase of the present tractor and every 12
months thereafter, he withdraws NAD5 000 from his account, to pay for
maintenance of the tractor. If he makes 5 such withdrawals, what will the new
monthly deposit be?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! this is what i get.
original cost of the tractor = 800,000.
tractor will be replaced in 5 years.
replacement cost is expected to increase 8% per year.
replacement cost in 5 years will be 800,000 * 1.08^5 = 1,1175,462.46, rounded to the nearest penny.
trade-in value on the original tractor will be 200,000 in 5 years.
the cash require to replace the tractor in 5 years, taking into account the trade-in value, will be 1,175,462.46 minus 200,000 = 975,462.46, rounded to the nearest penny.
when he bought the original tractor, he opened an account that will hold the money he will require to purchase the replacement tractor.
this account will be for 5 years with payments made at the end of every month with an interest rate of 12% compounded monthly.
the monthly rate on the account will be 1% per month.
he will need to have 975,462.46 in the account at the end of the investment period.
i used the calculator at https://arachnoid.com/finance/ to calculate the monthly payments required.
here are the results.
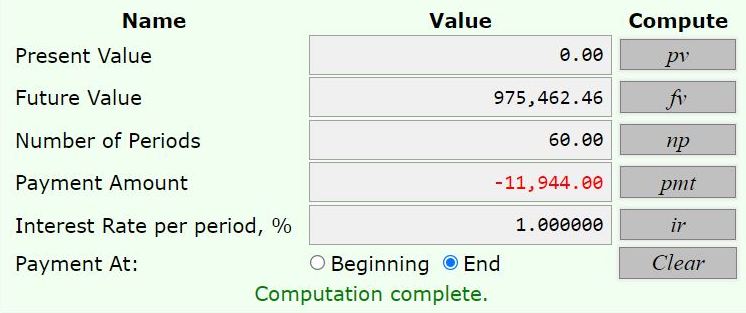
calculator says monthly payment required is equal to 11,944, rounded to the nearest penny.
he withdraws 5000 at the end of each year from this account to pay for maintenance on the existing tractor.
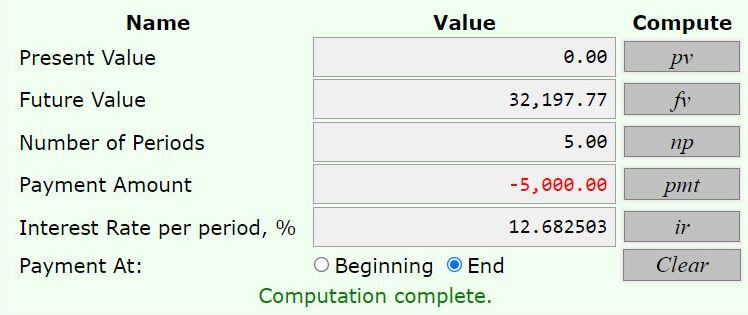
the future value of this 5000 withdrawn at the end of each year for 5 years is calculated using the same calculator used before.
the annual interest rate, however, needs to be adjusted to account for monthly compounding.
interest rate of 1% per month give an effective annual growth rate of 1.01 ^ 12 = 1.1268250301
subtract from that, and multiply it by 100, to get an effective annual interest rate of 12.68250301%.
that's the interest rate required to find the future value of the 5000 at the end of each year for 5 years.
this is because the account uses monthly compounding.
the calculator says that future value is equal to 31,764.24, rounded to the nearest penny.
the results from that calculator are shown below.
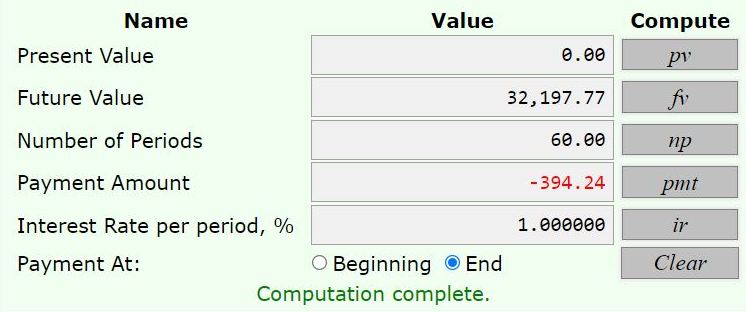
the equivalent monthly payments for a future value of 32,197.77 are then calculated.
they are equal to 394.24 as shown in the results from the calculator.
the annual interest rate of 12% was divided by 12, as was done in the original analysis, because we are dealing with monthly payments now, and not annual payments.
here are the results.
the payments have to be added because the total required to cover the costs to replace the machine are now the cost of the machine plus the annual expense that was required to maintain the original machine.
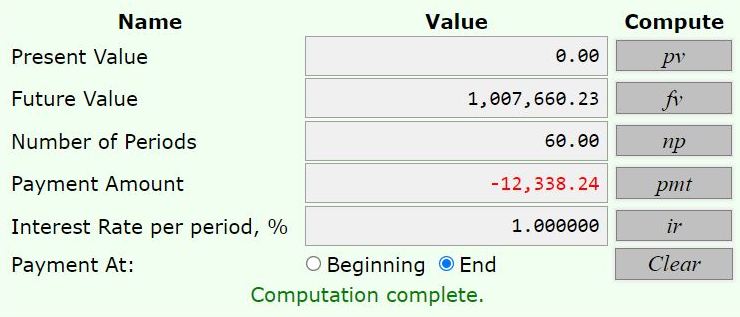
the total payments required at the end of each month becomes 11,944.00 + 394.24 = 12,338.24.
the future value required totals 975,462.46 + 32,197.77 = 1,007,660.23.
the combined payment and future value are shown in the results from the calculator.
here they are:
the combined monthly payment will cover the net cost of the replacement machinery plus the maintenance required on the original equipment for the 5 years that it is in operation.
i believe this answers what you need to provide as a solution to this problem.
let me know if you have any questions.
theo
|
|
|
| |