|
Question 1200256: Find the equation of the line through the point (6,6) and parallel to the point y=6-(x/2). Express the equation of the line in slope-intercept form, y=mx+b.
My first step was to put the (6,6) into y=mx+b
6=-(1/2)(6)+b -> 6=-(6/2)+b -> b=(18/2)? so then y=-(1/2)x+(18/2)
If someone wouldn't mind going over the work I would greatly appreciate it :)
Found 3 solutions by Alan3354, ikleyn, math_tutor2020:
Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website! Find the equation of the line through the point (6,6) and parallel to the point y=6-(x/2). Express the equation of the line in slope-intercept form, y=mx+b.
My first step was to put the (6,6) into y=mx+b
6=-(1/2)(6)+b -> 6=-(6/2)+b -> b=(18/2)? so then y=-(1/2)x+(18/2)
If someone wouldn't mind going over the work I would greatly appreciate it :)
-------------------------
Find the slope of y = 6-(x/2)
In slope-intercept form: y = (-1/2)x + 6
The slope is -1/2
Parallel lines have the same slope.
Use y-y1 = m*(x-x1) where m is the slope and (x1,y1) is the point
y-6 = (-1/2)*(x-6)
y = (-1/2)x + 9 --- same as your answer.
Answer by ikleyn(52781)  (Show Source):
Answer by math_tutor2020(3817)  (Show Source):
You can put this solution on YOUR website!
It's best to reduce 18/2 to 9.
Therefore, the answer would be y = (-1/2)x+9
As a check, plug the coordinates of (6,6) into that equation.
y = (-1/2)x+9
6 = (-1/2)*6+9
6 = -3+9
6 = 6
Both sides result in the same value, so we get a true equation.
This confirms (6,6) is on the line y = (-1/2)x+9
Furthermore, the two lines y = 6-(x/2) and y = (-1/2)x+9 are parallel since they have the same slope -1/2.
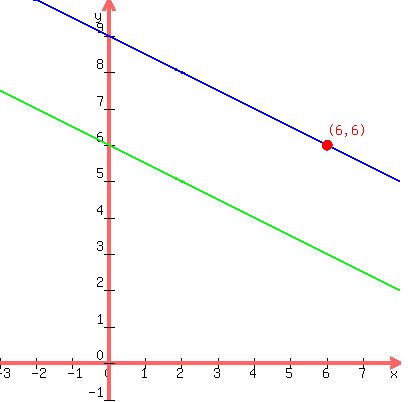
y = 6-(x/2) in green
y = (-1/2)x+9 in blue
I recommend using a tool like Desmos or GeoGebra to graph.
|
|
|
| |
