|
Question 1199205: find the missing value of the line that passes through (R,2) and (5,3) and has a slope of 1/2
Found 4 solutions by josgarithmetic, ikleyn, greenestamps, math_tutor2020:
Answer by josgarithmetic(39618)   (Show Source):
Answer by ikleyn(52794)  (Show Source):
You can put this solution on YOUR website! .
Using coordinates of the points, write equation for the slope
 =  .
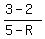From this equation, find the unknown value of R. For it, first cross-multiply; then simplify
2*(3-2) = 5 - R
2 = 5 - R
R = 5 - 2 = 3.
ANSWER. R = 3.
Solved.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
To work a problem like this, I encourage students to think informally, using the concept of slope as rise over run. A student can get a better understanding of HOW he is solving the problem by doing that, instead of plugging numbers and variables into the formal formula for finding the slope between two points.
In this problem, the two points are (R,2) and (5,3).
The rise is from 2 to 3, a difference of 1.
If the slope (rise over run) is 1/2 and the rise is 1, then the run must be 2.
If the run from R to 5 is 2, then R must be 5-2=3.
ANSWER: R is 3
Answer by math_tutor2020(3817) (Show Source):
You can put this solution on YOUR website!
A visual approach:
Plot the point (5,3) on the xy grid.
The slope 1/2 tells us to "go up 1, then to the right 2 units".
This is because:
slope = rise/run = 1/2
rise = 1 = go up 1
run = 2 = go to the right 2
If we started at (5,3) and did the "up 1, right 2" movement pattern, then we'll arrive at (7,4). See the graph below.
But we want the y coordinate to be 2 instead of 4. I'm referencing the point (R,2).
Let's reverse the "up 1, right 2" process.
Instead we'll follow "down 1, left 2".
Again we start at the anchor (5,3).
Move down 1, left 2 to arrive at (3, 2) which shows that R = 3
Graph:
The green line represents the linear equation y = 0.5x+0.5
1/2 = 0.5
|
|
|
| |
