|
Question 1196766: Hi! I need help for a project so I could take my final exam. I would really appreciate all the help I could get. Thank you so much.
Problem: Blue strand wire rope is the top seller of the company. TSD has to make a production schedule. To create product a blue strand wire rope, 3 machines are need. For wire rope #1 (BSWR 6x36 IWRC), it needs 19 coils of wires and 3 hours of production, while for wire rope #2 (BSWR 6x19 IWRC), 14 coils of wires and 4 hours of production. Wire rope #1 is sold for PhP 64,500 while wire rope #2 is sold for PhP 10,500. How many rolls of wire rope #1 and #2 does TSD has to schedule in the production to maximize the monthly sales while being limited to 6 machines, 2,006 coils of wires and 1,248 hours production?
VARIABLES:
Wire Rope #1
3 machines
19 coils of wire
3 hours of production
PhP 64,500 selling price
Wire Rope #2
3 machines
14 coils of wire
4 hours of production
PhP 10,500 selling price
CONSTRAINTS
6 machines
2,006 coils of wires
1,248 hours of production
OBJECTIVE FUNCTION:
Max: 64,500X1 + 10,500X2
Subject to: 1X1 + 1X2 = 6
19X1 + 14X2 ≤ 2,006
3X1 + 4X2 ≤ 1,248
X1 ≥ 0
X2 ≥ 0
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
From the first glance, this problem is the kind of the Linear Programming optimization.
But in reality, it is for totally different method of solution: it is to apply the COMMON SENSE.
First, let's organize the given info into this TABLE. m-hours stands for machine-hours.
one product one product
of wire roop #1 of wire roop #2
3 machine 3 machine
19 coils of wires 14 coils of wires
3 m-hours production 4 m-hours production
sold for PhP 64500 each sold for PhP 10500 each
Resources: 2006 coils of wires
and 1248 machine-hours.
Let six mashines be A, B, C, D, E and F. So, we have two triples of machines ABC and DEF.
The rate of making money is
three machines making product #1: 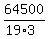 = 1131.579 of PhP per coil per hour.
three machines making product #2: = 1131.579 of PhP per coil per hour.
three machines making product #2: 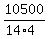 = 187.5 of PhP per coil per hour.
It makes it clear that the most agressive strategy is THIS
+-------------------------------------------------------------------------------------------+
| 3 machine (A,B,C) work as long as possible and produce as many wire roop #1 as possible. |
| (To produce one product #1, they consume 19 coils and 3 m-hours). |
| |
| 3 machine (D,E,F) work as long as possible and produce as many wire roop #1 as possible. |
| (To produce one product #1, they consume 19 coils and 3 m-hours). |
+-------------------------------------------------------------------------------------------+
Thus, doing this way, 6 machines produce 2 products #1 and consume 19+19 = 38 coils and 3+3 = 6 m-hours.
Which resourse will run out first - machine-hours or coils ?
coils: 2006/38 = 52 + 30/38 (<<<---=== division with the remainder)
m-hours: 1248/6 = 208
Thus, coils of wires will run out first.
+--------------------------------------------------------------------------------+
| Let's call this cycle "consuming 3+3 = 6 m-hours, 6 machines produce |
| 2 products #1 and consume 19+19 = 38 coils of wires" |
| as "one basic cycle". |
+--------------------------------------------------------------------------------+
Thus we found out that the "basic cycle" can be repeated (cycled) 52 times.
After that, the remaining resources are 30 coils of wires and 1248 - 6*52 = 936 m-hours.
With these remaining resources, we can (and we) run only 3 machines ABC to produce one #1 product.
They will spend 19 coils of wire and 3 m-hours.
The remaining resource is 30-19 = 11 coils of wire and 936-3 = 933 m-hours,
that we can not use: it is useless remaining resource.
The final conclusion and the ANSWER is that we run two triples of the machines
only to produce 2*52 + 1 = 105 of products #1; we do not make product #2, at all.
The earning of this strategy is 105*64500 = 6772500 dollars.
The remaining unused resource is 1248 - 3*105 = 933 m-hours and 2006 - 19*105 = 11 coils of wires. = 187.5 of PhP per coil per hour.
It makes it clear that the most agressive strategy is THIS
+-------------------------------------------------------------------------------------------+
| 3 machine (A,B,C) work as long as possible and produce as many wire roop #1 as possible. |
| (To produce one product #1, they consume 19 coils and 3 m-hours). |
| |
| 3 machine (D,E,F) work as long as possible and produce as many wire roop #1 as possible. |
| (To produce one product #1, they consume 19 coils and 3 m-hours). |
+-------------------------------------------------------------------------------------------+
Thus, doing this way, 6 machines produce 2 products #1 and consume 19+19 = 38 coils and 3+3 = 6 m-hours.
Which resourse will run out first - machine-hours or coils ?
coils: 2006/38 = 52 + 30/38 (<<<---=== division with the remainder)
m-hours: 1248/6 = 208
Thus, coils of wires will run out first.
+--------------------------------------------------------------------------------+
| Let's call this cycle "consuming 3+3 = 6 m-hours, 6 machines produce |
| 2 products #1 and consume 19+19 = 38 coils of wires" |
| as "one basic cycle". |
+--------------------------------------------------------------------------------+
Thus we found out that the "basic cycle" can be repeated (cycled) 52 times.
After that, the remaining resources are 30 coils of wires and 1248 - 6*52 = 936 m-hours.
With these remaining resources, we can (and we) run only 3 machines ABC to produce one #1 product.
They will spend 19 coils of wire and 3 m-hours.
The remaining resource is 30-19 = 11 coils of wire and 936-3 = 933 m-hours,
that we can not use: it is useless remaining resource.
The final conclusion and the ANSWER is that we run two triples of the machines
only to produce 2*52 + 1 = 105 of products #1; we do not make product #2, at all.
The earning of this strategy is 105*64500 = 6772500 dollars.
The remaining unused resource is 1248 - 3*105 = 933 m-hours and 2006 - 19*105 = 11 coils of wires.
Solved.
--------------------
It would be interesting to me to get your feedback.
|
|
|
| |