SOLUTION: Prove by induction that 2^n>2n gor every positive integer n>2.

Algebra ->  Linear-equations -> SOLUTION: Prove by induction that 2^n>2n gor every positive integer n>2.       Log On


   

Question 1188707: Prove by induction that 2^n>2n gor every positive integer n>2.
Answer by ikleyn(52788) About Me  (Show Source):
You can put this solution on YOUR website!
.
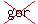Prove by induction that 2^n > 2n cross%28gor%29 for every positive integer n > 2.
~~~~~~~~~~~~~~~~~ 

(1)  Base case n= 3.

     Then  2%5E3 = 8,  and 8 > 2*3 = 6;  so the base of induction is established.



(2)  The induction step from n to (n+1), for n > 2.


     So we assume that 2%5En > 2n  for some positive integer n > 2.


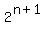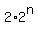     We have  2%5E%28n%2B1%29 = 2%2A2%5En = 2%5En + 2%5En.           (1)


     According to the induction assumption,  2%5En > 2n,  so we can continue the preceding line in this way

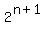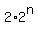         2%5E%28n%2B1%29 = 2%2A2%5En = 2%5En + 2%5En > 2n + 2n.      (2)


     Next, we can continue this way

         2n + 2n = 2*(n+1) + 2(n-1),  and since  n > 2, the last addend is positive.


     THEREFORE,  2n + 2n > 2*(n+1)  for n > 2.         (3)


     Combining all these parts (1), (2) and (3) together, we have

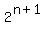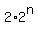          2%5E%28n%2B1%29 = 2%2A2%5En = 2%5En + 2%5En > 2n + 2n > 2*(n+1)  for n > 2.


     Thus the proof for the inductive step  n ---> (n+1)  is complete.



(3)  Due to the principle of Mathematical induction, the statement is proved for all positive integer n.

Solved.