SOLUTION: Prove by induction and through divisibility algorithm that 11^n - 6 is divisible by 5 for every positive integer n.

Algebra ->  Linear-equations -> SOLUTION: Prove by induction and through divisibility algorithm that 11^n - 6 is divisible by 5 for every positive integer n.      Log On


   

Question 1188706: Prove by induction and through divisibility algorithm that 11^n - 6 is divisible by 5 for every positive integer n.
Answer by ikleyn(52786) About Me  (Show Source):
You can put this solution on YOUR website!
.
Prove by induction and through divisibility algorithm that 11^n - 6 is divisible by 5 for every positive integer n.
~~~~~~~~~~~~~~~~~ 


(1)  Base case n= 1.

     Then 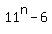 11%5En-6 = 11 - 6 = 5  is divisible by 5,  so the base of induction is established.



(2)  The induction step from n to (n+1).


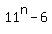     We assume that  11%5En-6  is divisible by 6 for some integer positive index n.


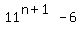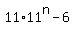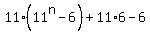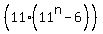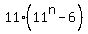     Then  11%5E%28n%2B1%29-6 = 11%2A11%5En+-+6+ = 11%2A%2811%5En-6%29+%2B+11%2A6+-+6 = %2811%2A%2811%5En-6%29%29 + (66-6) = 11%2A%2811%5En-6%29 + 60.


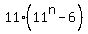     The addend  11%2A%2811%5En-6%29  is divisible by 5 due to the inductive assumption, and the term 60 is also divisible by 5.


     Thus the inductive step from n to (n+1) is complete.



(3)  Due to the principle of Mathematical induction, the statement is proved for all positive integer n.

Solved.


/////////////


Above was the proof by induction.

Below is more simple proof using the divisibility by 5 rule. 


The number 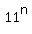 11%5En  has the last (the units) digit  1 (one).


When we subtract 6 from this number, we get the last digit 5 for the difference,

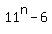which means that this difference,  11%5En-6,  is divisible by 5 without a remainder.

Solved  (twice,  by two different methods).