|
Question 1188643: If A(3,6) and C(-1,2) are two vertices of a rhombus ABCD, then find the equation of straight line that lies along the diagonal BD.
Answer by ikleyn(52782)   (Show Source):
You can put this solution on YOUR website! .
If A(3,6) and C(-1,2) are two vertices of a rhombus ABCD, then find the equation of straight line that lies along the diagonal BD.
~~~~~~~~~~~~~~~~~~~
The STRATEGY
(1) First find an equation of the line AC;
(2) then find the midpoint of the segment AC;
(3) then find an equation of the perpendicular line passing through this midpoint.
IMPLEMENTATION
(1) To find an equation of the line AC, first find its slope: m = 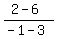 =  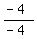= 1.
Hence, an equation of the line AC is y-6 = 1*(x-3), or y-6 = x-3, or y - x = 3.
(2) The midpoint of the segment AC is (1,4) (the mean values for each pair of co-named coordinates).
(3) The perpendicular line to AC is x + y = const = 1 + 4 = 5.
ANSWER. The sough equation is x + y = 5 (or any other equation, equivalent to it . . . )
Solved.
|
|
|
| |
