|
Question 1187223: A factory manufactures two types of gadgets, regular and premium. Each gadget requires the use of two operations, assembly and finishing, and there are at most 12 hours available for each operation. A regular gadget requires 1 hour of assembly and 2 hours of finishing, while a premium gadget needs 2 hours of assembly and 1 hour of finishing. Due to other restrictions, the company can make at most 7 gadgets a day. If a profit of $20 is realized for each regular gadget and $30 for a premium gadget, how many of each should be manufactured to maximize profit?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! let x equal the number of regular gadgets.
let y equal the number of premium gadgets.
a regular gadget requires 1 hour of assembly and 2 hours of finishing.
a premium gadget requires 2 hours of assembly and 1 hour of finishing.
assembly and finishing have at most 12 hours available for each.
inequalities for assembly and finishing are:
x + 2y <= 12 for assembly
this is because a regular gadget requires one hour for assembly while a premium gadget requires 2 hours for assembly.
2x + y <= 12 for finishing.
this is because a regular gadget requires 2 hours for finishing while a premium gadget requires 1 hours for finishing
another inequality is:
x + y <= 7
this because the most number of gadgets, regardless of type, that can be built in a day is 7.
the profit for a regular gadget is 20 dollars a unit and the profit for a premium gadget is 30 dollars a unit.
the equation for this is profit = 20x + 30y
this is the objective function.
using the desmos.com calculator, you will graph the opposite of the inequalities to find the region of feasibility.
the region of feasibility is the unshaded portion of the graph.
you will then evaluate the objective function at each of the corner points of the feasible region to find the maximum profit.
you will also check the constraint inequalities at the maximum profit point to make sure that all the constraints have been met.
the graphing software used can be found at https://www.desmos.com/calculator
here's what the graph looks like.
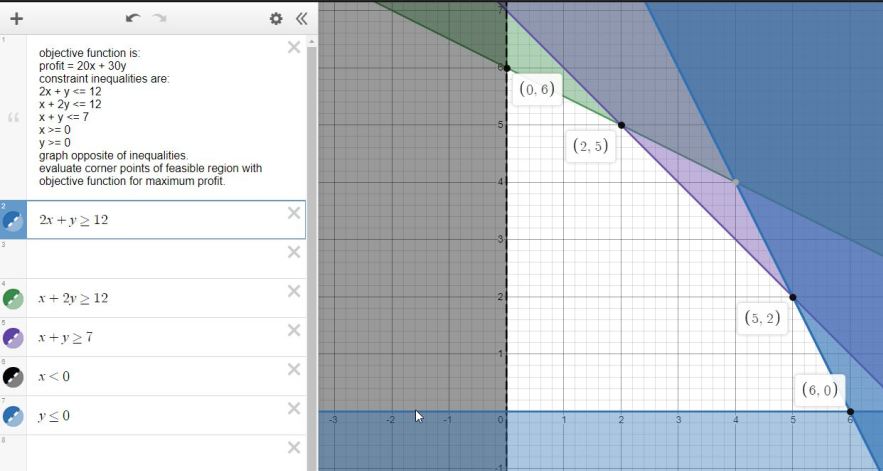

maximum profit is at (2,5) = 20 * 2 + 30 * 5 = 190.
all constraints are satisfied at maximum profit point as shown below:
2x + y <= 12 becomes 2*2 + 5 = 4 + 5 = 9 <= 12.
x + 2y <= 12 becomes 2 + 2*5 = 2 + 10 = 12 <= 12.
x + y <= 7 becomes 2 + 5 = 7 <= 7.
x >= 0 is true.
y >= 0 is true.
solution is that maximum profit is obtained when 2 regular and 5 premium gadgets are produced and sold.
|
|
|
| |