|
Question 1183948: A line tangent to the curve x = y^(1/2) at the point P intersects the x axis at
the point Q.
If P travels up the curve at a rate of 2 units per second, how fast is the point
Q traveling when P passes through the point (2,4)?
Found 2 solutions by Edwin McCravy, robertb:
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
 Suppose the line is tangent to the curve at P(h,h2).
Then its slope is the derivative of
Suppose the line is tangent to the curve at P(h,h2).
Then its slope is the derivative of  at P(h,h2).
The derivative is at P(h,h2).
The derivative is  , so the slope at P(h,h2) is 2h.
Since it goes through (h,h2), its equation is: , so the slope at P(h,h2) is 2h.
Since it goes through (h,h2), its equation is:
 Its x-intercept P is the x-value when y=0, so
Its x-intercept P is the x-value when y=0, so

 Divide through by h
Divide through by h


 So the coordinates of Q are
So the coordinates of Q are 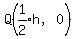 . .
 Now let's switch the letter h to x. [It would have been too confusing
if we had started out with x because the equation of a line uses x).
Now let's switch the letter h to x. [It would have been too confusing
if we had started out with x because the equation of a line uses x).
 We want to know how fast Q is moving. Since Q is on the x-axis, Q moves the
same speed as its own x-coordinate
We want to know how fast Q is moving. Since Q is on the x-axis, Q moves the
same speed as its own x-coordinate 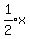 . So let the variable
q = the x-coordinate of Q. . So let the variable
q = the x-coordinate of Q.  . We want to know . We want to know  at P(2,4) which is when x=2.
The point P moves up the curve at the rate of 2 units per second, so at P(2,4) which is when x=2.
The point P moves up the curve at the rate of 2 units per second, so











 Evaluating that when x=2,
Evaluating that when x=2,
  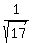 units per second.
Edwin units per second.
Edwin
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! *
If  , then , then  , or , or 
If we let point P be ( , ,  ), then the tangent line is ), then the tangent line is
 , whose x-intercept is obtained by letting y = 0: , whose x-intercept is obtained by letting y = 0:
 ===> ===>  <===> <===>  ===> ===>  . .
===> With respect to time,  , or , or  . .
Now the arc length "s" from x = 0 to x =  is given by is given by
 . .
===>  , by a direct application of the fundamental theorem of calculus. , by a direct application of the fundamental theorem of calculus.
===>  . .
Since at the instant when P=(2,4)  , we get , we get
 , so that , so that  unit per second, unit per second,
the rate of change of the x-intercept Q.
|
|
|
| |