SOLUTION: Minimize z=4x+7y subject to x-y>1,3x+2y>18,x>0,y>0

First inequality x-y > 1 is THIS restriction

     y < x - 1.


Second inequality 3x+2y > 18 is THIS restriction

    y > .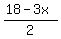


Together with the inequalities x > 0, y > 0 they form THIS feasibility domain in the first quadrant QI, shown in the Figure below:


    


    Plot y < x-1 (under the read line) and  y > 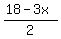 (over the green line)



Feasibility domain is INFINITE AREA in Q1 UNDER the red line and over the green line.


Notice that x-axis  y= 0 is not included into the feasibility domain since we have strict inequality y > 0 given.


The red and the green lines ALSO are not included into the feasibility domain, since the given inequalities are strict inequalities.


It implies that the given objective function HAS NO minimum in the assigned domain:


      for any point in the domain, there is another point in the domain
      where the objective function has lesser value.


ANSWER.  With given restrictions, the posted problem HAS NO SOLUTION.