|
Question 1167928: The graph of the line through (2, 3) that is perpendicular to the line with
equation x = -1 also goes through which point?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the line with equation x = -1 is a vertical line.
when x = -1, the value of y can be any real value.
(-1,0) is on the line.
(-1,3) is on the line.
etc.
the slope of a vertical line is undefined.
that's because the slope of a straight line is the change in the value of y divided by the corresponding change in the value of x.
since x is always equal to -1, there is no change in the value of x, meaning the change in the value of x is equal to 0.
this means that the denominator in the equation of change in the value of y divided by the change in the value of x is equal to the change in the value of y divided by 0, the result of which is undefined.
the line perpendicular to the vertical line has a slope that is a negative reciprocal of the slope of the vertical line.
if the slope of the vertical line is the change in the value of y divided by 0, then the slope of the line perpendicular to it is equal to 0 divided by the negative value of the change in the value of y.
the slope of the horizontal line is therefore equal to 0, because 0 divided by anything is equal to 0.
that means the line is horizontal.
the slope intercept form of the equation of a straight line is y = mx + b
m is the slope
b is the y-intercept.
with a slope of 0, the equation of the horizontal line is therefore y = 0 * x + b
solve for b by replacing x and y with their respective values from any point on the line.
when the line goes through the point (x,y) = (2,3), replace x with 2 and y with 3 to get:
y = 0 * x + b becomes:
3 = 0 * 2 + b
simplify to get b = 3
the equation of the line perpendicular to the vertical line is therefore:
y = 0 * x + 3 which simplifies to y = 3.
the graph of both lines is shown below:
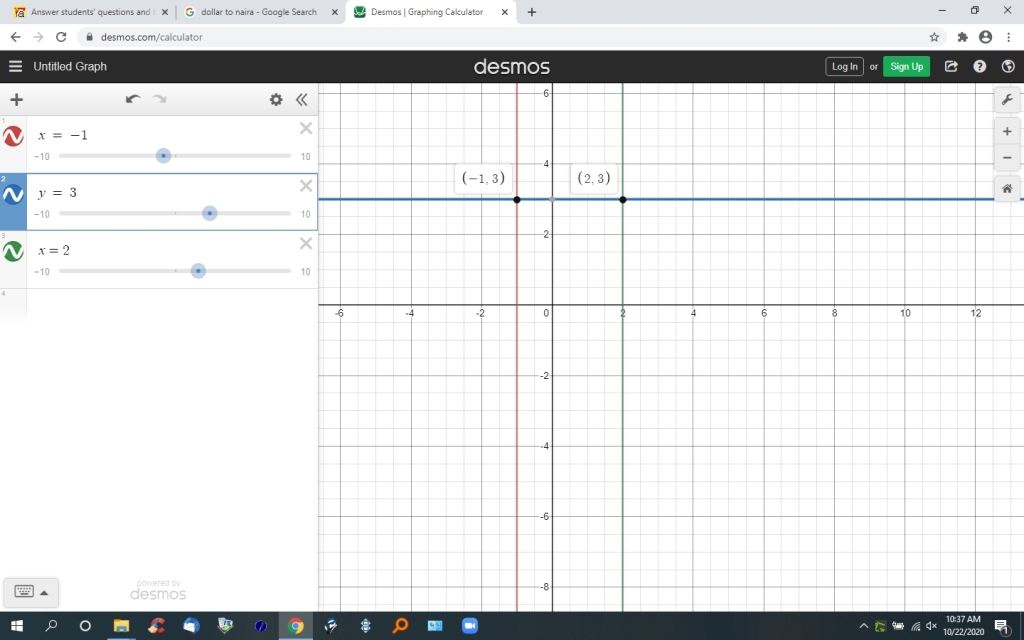
you can see from the graph that the lines intersect at the point (x,y) = (-1,3) and that the point (x,y) = (2,3) is on the horizontal line.
|
|
|
| |