|
Question 1167433: Given f(x) = −x^6 + 5x^5 − 4x^3 + 12x
(a) What is the leading term of f(x)?
(b) What is the degree of f(x)?
(c) Describe the end behavior of f(x) by finding:
lim F(x)=
x→−∞
lim f(x) =
x→∞
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the leading term of f(x) is equal to -x^6.
the degree of f(x) is 6 because the term with the largest exponent is -x^6.
the end behavior of f(x) is determined by the leading term after the expression has been ordered by descending order of degree.
the leading term is -x^6.
the leading term will always be negative because x^6 will always be positive and therefore -x^6 will always be negative, no matter what the value of x is.
this says that, as x approaches plus infinity, -x^6 will be negative, and as x approaches minus infinity, -x^6 will be negative.
you can graph the equation and the graph will show you that this is true.
see below for the graph.

the graph shows that y reaches a maximum value of 818.023 when x = 4.052.
the graph shows the value of y gets more and more negative as x gets more and more negative and the value of y more and more negative as x gets more and more positive.
note that y = f(x), so the equation can be shown as y = ..... and the same equation can be shown as f(x) = .....
you can use the equation to determine that this is true.
the equation is f(x) = −x^6 + 5x^5 − 4x^3 + 12x
when x = 8,000,000, f(x) = -2.62143836 * 10 ^ 41.
when x = -8,000,000, f(x) = -2.62144164 * 10 ^ 41.
the result is negative in both cases.
you can raise the value of x as much as you want and the result will be negative.
you can lower the value of x as much as you want and the result will be negative.
that's your end behavior of f(x).
here's a reference on the end behavior of a polynomial.
https://www.purplemath.com/modules/polyends.htm
to summarize the rules.
if the polynomial is in the form of f(x) = some expression of x, then:
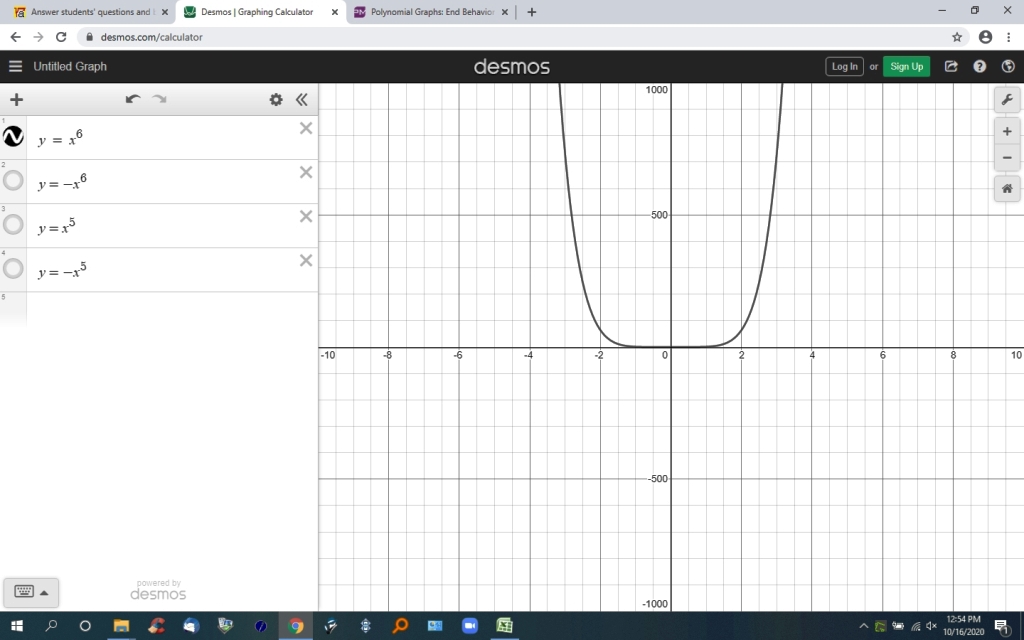
if the degree of the polynomial is even and the coefficient of the leading term is positive, then the end behavior of the polynomial is positive on both ends.
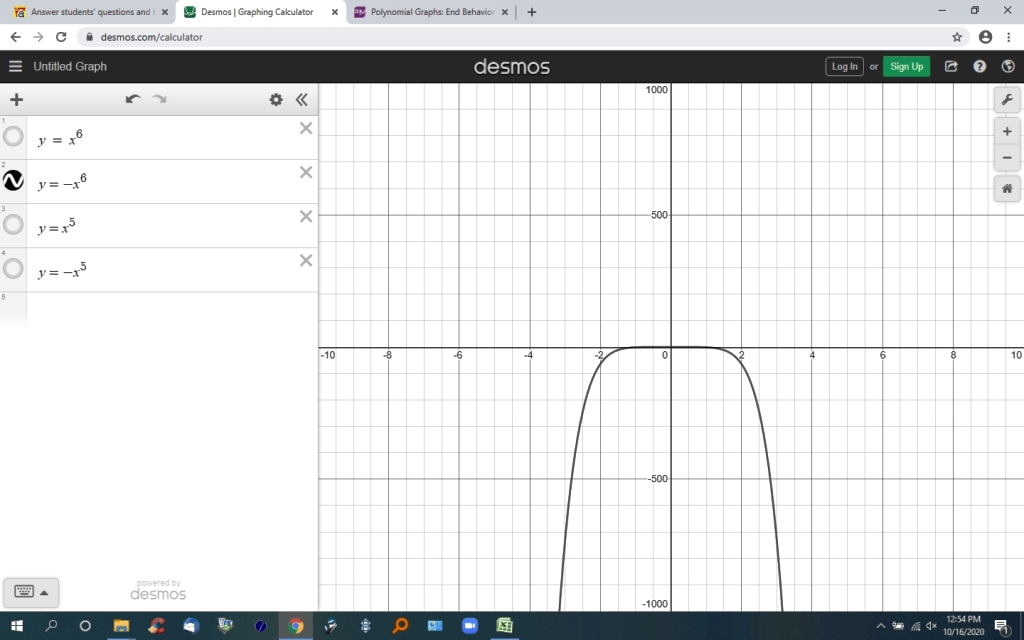
if the degree of the polynomial is even and the coefficient of the leading term is negative, then the end behavior of the polynomial is negative on both ends.
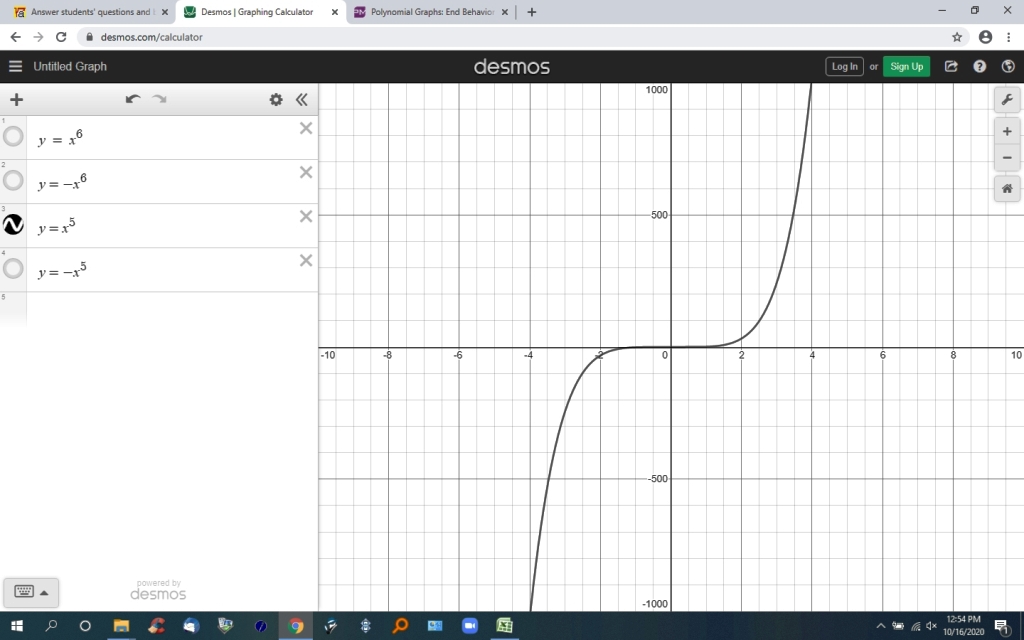
if the degree of the polynomial is odd and the coefficient of the leading term is positive, then the end behavior of the polynomial is negative on the left end and positive on the right end.
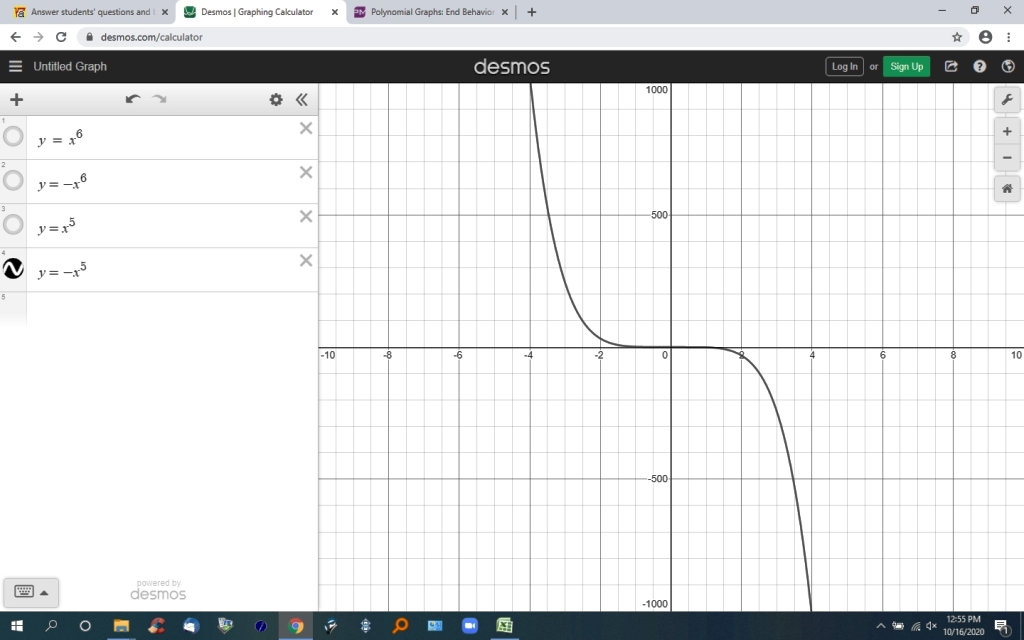
if the degree of the polynomial is odd and the coefficient of the leading term is negative, then the end behavior of the polynomial is positive on the left end and negative on the right end.
since the leading term is the controlling factor as to which way the end behavior goes, i can use a simple graph to show you.
the first graph is a leading term with a positive coefficient and an even power.
the second graph is a leading term with a negative coefficient and an even power.
the third graph is a leading term with a positive coefficient and an odd power.
the fourth graph is a leading term with a negative coefficient and an odd power.
here they are:
a very good reference on the behavior of polynomials can be found at:
https://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/col_alg_tut35_polyfun.htm
this reference has a wealth of information about how polynomials behave when they're graphed.
to repeat what i think i said before.
if the argument of the function is x, then:
the degree of the function is the term with the largest degree.
the term with the largest degree is the term that contains x raised to the largest exponent.
the leading term is the term with the largest degree.
|
|
|
| |