SOLUTION: What is the area of a triangle whose vertices are A(2,-4), B(1,6) and C(-8,3)?

Algebra ->  Linear-equations -> SOLUTION: What is the area of a triangle whose vertices are A(2,-4), B(1,6) and C(-8,3)?      Log On


   

Question 1166942: What is the area of a triangle whose vertices are A(2,-4), B(1,6) and C(-8,3)?
Answer by greenestamps(13198) About Me  (Show Source):
You can put this solution on YOUR website!


Use the shoelace method (do an internet search for explanations and video demonstrations).

The area of the triangle is one-half the absolute value of the determinant of the matrix consisting of the coordinates of each point in each column, starting and ending with one of the points (to make a complete circuit of the vertices).

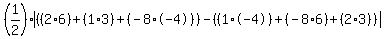
A+=+abs%28%281%2F2%29%28matrix%282%2C4%2C2%2C1%2C-8%2C2%2C-4%2C6%2C3%2C-4%29%29%29 =

You can finish the calculations from there.

Alternatively (it will take much longer) you can form a rectangle with vertical and horizontal sides just enclosing the triangle; with the given triangle, the rectangle will be formed by the lines x=-8, x=2, y=-4, and y=6.

Then the area of the given triangle can be calculated as the area of the rectangle, minus the areas of the three triangles inside the rectangle and outside the given triangle.