|
Question 1165245: Mark manages a store that sells cell phones. Each MX300 takes 6 hours to create the plastic pieces, 2 hours to create the electronics, and 10 hours of labor to assemble the final product. Each XL2000 requires 3 hours to create the plastic pieces, 4 hours to create the electronics, and 21 hours of labor to assemble the final product. The factory has 840 hours to create the plastic pieces, 360 hours to create the electronics, and 1880 hours of labor to assemble the final product each week. If each MX300 generates $4 in profit, and each XL2000 generates $19, how many of each of the cell phones should Mark have the store sell each week to make the most profit?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! use the linear programming tool at https://www.zweigmedia.com/RealWorld/simplex.html
your objective function is p = 4x + 19y
x represents the number of mx300 units.
y represents the number of xl200 units.
your constraint functions are:
6x + 3y <= 840 for number of hours to create the pieces.
2x + 4y <= 360 for number of hours to create the electronics.
10x + 21y <= 1880 for number of hours to assemble the final product.
x,y >= 0
your inputs to the simplex method tool and outputs from the simplex method tool are shown below:
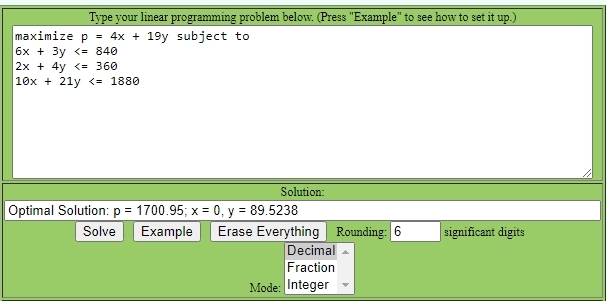
you evaluate your objective function at x = 0 and y = 89.5238
your objective function is p = 4x + 19y.
this becomes 0 * 4 + 19 * 89.5238 = 1700.95 rounded to 2 decimal places as shown in the optimal solution.
all the constraints have to be satisfied:
6x + 3y <= 840 becomes 6 * 0 + 3 * 89.5238 <= 840 which becomes 268.5714 <= 840 which is true.
2x + 4y <= 360 becomes 2 * 0 + 4 * 89.5238 <= 360 which becomes 358.0952 <= 360 which is true.
10x + 21y <= 1880 becomes 10 * 0 + 21 * 89.5238 which becomes 1879.9998 <= 1880 which is true.
x >= 0 becomes 0 >= 0 which is true.
y >= 0 becomes 89.5238 >= 0 which is true.
all the constraints are satisfied, so the solution is good.
|
|
|
| |