SOLUTION: Find the quadratic polynomial whose graph passes through the points (1,14) (2,28) (3,48)

Algebra ->  Linear-equations -> SOLUTION: Find the quadratic polynomial whose graph passes through the points (1,14) (2,28) (3,48)       Log On


   

Question 1161075: Find the quadratic polynomial whose graph passes through the points (1,14) (2,28) (3,48)
Found 3 solutions by MathLover1, solver91311, greenestamps:
Answer by MathLover1(20849) About Me  (Show Source):
You can put this solution on YOUR website!
y=ax%5E2%2Bbx%2Bc use given point (1,14)
14=a%2A1%5E2%2Bb%2A1%2Bc
14=a%2Bb%2Bc ......solve for c
c=14-a-b.........eq.1
y=ax%5E2%2Bbx%2Bc use given point (2,28)
28=a%2A2%5E2%2Bb%2A2%2Bc
28=4a%2B2b%2Bc ......solve for c
c=28-4a-2b.........eq.2
from eq.1 and eq.2 we have
14-a-b=28-4a-2b.....solve for b
2b-b=28-4a%2Ba-14
b=14-3a.........eq.3
go to
c=14-a-b.........eq.1, substitute b
c=14-a-%2814-3a%29
c=14-a-14%2B3a
c=2a...............eq.4

go to
y=ax%5E2%2Bbx%2Bc use given point (3,48), substitute b from eq.3 and c from eq.4
48=a%2A3%5E2%2B%2814-3a%29%2A3%2B2a ........solve for a
48=9a%2B42-9a%2B2a.....simplify
48=42%2B2a
48-42=2a
2a=6
highlight%28a=3%29
go to
b=14-3a.........eq.3, substitute a
b=14-3%2A3
highlight%28b=5%29
go to
c=2a...............eq.4, substitute a
c=2%2A3
highlight%28c=6%29
your equation is:
y=3x%5E2%2B5x%2B6







Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!


A quadratic polynomial function has the form:



Any point on the graph of this function has the form



So, if the point is on the graph, then the following must hold:



Similarly, for and



and



must hold.

These three equations reduce to the 3X3 linear system: 
              a  +  b  +  c  =  14

             4a  + 2b  +  c  =  28

             9a  + 3b  +  c  =  48


Solve the system for the required , , and coefficients.


John

My calculator said it, I believe it, that settles it

Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


The standard method for solving a problem like this is as shown by the other two tutors: use the x and y coordinates of the given points in the standard equation ax%5E2%2Bbx%2Bc to get three equations in the coefficients a, b, and c; then solve the system of equations.

Here is a completely different method that I find a bit less work. This alternative method can be used because the y values are given for three consecutive x values.

So think of the problem as a sequence of numbers produced by a quadratic polynomial.

In a sequence produced by the quadratic polynomial ax%5E2%2Bbx%2Bc, the second differences are the constant 2a. (If you know some basic calculus, you can see that is true, since the second derivative of the polynomial is 2a.)

In this sequence, the second difference is 6:
   14  18  48
     14  20
        6

Since we now that second difference is 2a, we know that the leading coefficient a is 3, and the quadratic polynomial is

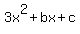
3x%5E2%2Bbx%2Bc

The "bx+c" is a linear polynomial; it can be determined easily by comparing the actual y values to the value of 3x^2:
   x   3x^2   y   y-3x^2 (= bx+c)
  -------------------------------
   1     3   14     11
   2    12   28     16
   3    27   48     21

It is easy to see that the values in the last column are bx+c = 5x+6.

So, already knowing that the leading term of the quadratic is 3x^2, we now know that the complete quadratic is

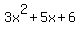
3x%5E2%2B5x%2B6