SOLUTION: Find the slope of the tangent line to the graph of the function at the given point. f(x) = 9x − 4x^2 at (−2, −34) m = Determine an equation of the tangent line. y =

The slope of the tangent line of f(x) at x=k is equal to the derivative f'(x) evalated at k:



f(x) =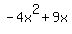 

f'(x) =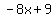 



f'(x) at x = -2:  f'(-2) = -8(-2) + 9 = 25



The slope of the tangent line at (-2,-34) is therefore  





For the equation of the tangent line, make use of the point-slope form of a line, and the given information that the line passes through (-2,-34):



   y - y0 = m(x-x0)  

  y-(-34) = 25(x-(-2))

  y+34 = 25x+50

     in slope-intercept form