|
Question 1148227: A new high school math project is being tested in the state. In the first year (year 1), there are 671 students involved. By the end of the third year (year 3), 12487 students are expected to be involved. Assuming the increase is linear, write the equation of the line, in slope-intercept form, representing the number of students participating in this project for each year x. Use this result to predict the number of students involved at the end of 5 years.
Hint: Use the ordered pairs (1, 671) and (3, 12487).
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the slope intercept form of a straight line equation is:
y = mx + b
m is the slope
b is the y-intercept.
you have two points to use.
they are:
(1,671)
(3,12487)
m is the slope and is equal to (12487 - 671) / (3 - 1) = 5908.
the slope intercept form of the equation becomes:
y = 5908 * x + b
in this equation, x represents the year.
the first year becomes x = 0
the third year becomes x = 2
your coordinate points becomes (x,y) = (0,671) and (2,12487).
this a translation from (year, number of students) = (1,671) and (3,12487)
when year = 1, x = 0
when year = 3, x = 2
using the point (x,y) = (0,671), we find b to be equal to 671, because the y intercept is the value of y when x is equal to 0.
if we had used the point (2,12487), we would have solved for b as follows:
y = 5908 * x + b becomes 12487 = 5908 * 2 + b
we would solve for b to get b = 12487 - 2 * 5908 = 12487 - 11816 = 671.
both points lead to the same value of b, as they should.
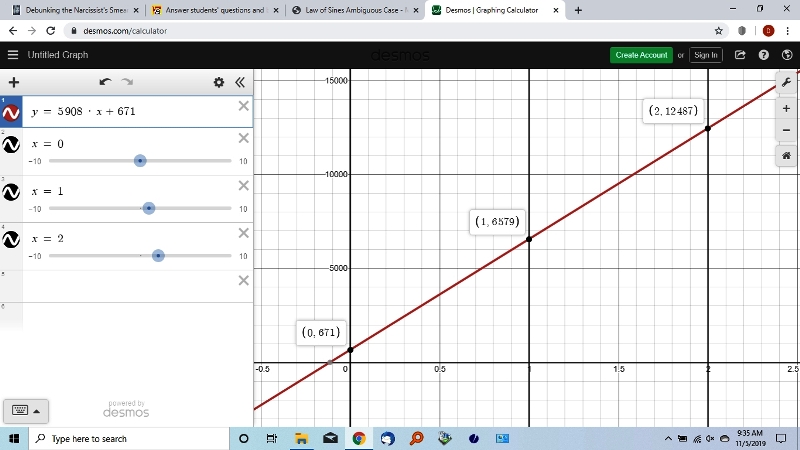
the equation becomes y = 5908 * x + 671.
when x = 0, y = 671
when x = 1, y = 5908 * 1 + 671 = 6579
when x = 2, y = 5908 * 2 + 671 = 12487.
this equation can be graphed as shown below:
|
|
|
| |