SOLUTION: The solution to a system of two linear equations is (4,-3). One equation has a slope of 4. The slope of the other line is the negative reciprocal of the slope of the first. Find

We can write the first equation in the form


    y = 4x + c,    (1)


where "c" is some constant term, now unknown.

In this form, the line (1) has exactly the slope 4.


To find the value of "c", use the fact that the point (4,-3) is the solution.

It means that the expression (1) should become an identity at x= 4, y= -3.

So, substitute x= 4, y= -3 into (1), You will get

    -3 = 4*4 + c,

which implies  c= -3 - 4*4 = -3 - 16 = -19.



Now you know the first equation in all details.  It is

     y = 4x - 19.    (2)



The slope of the other line is , according to the condition.

So, it has the form


    y = ,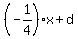


where "d" is another constant term.


To find "d", use again the fact that the point (4,-3) is the solution to the system.

Again, as we did it above, substitute x= 4, y= -3 into expression (3). You will get

    -3 = 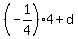,    (3)

which implies

    -3 = -1 + d.


Thus d = -3 + 1 = -2.


Therefore, your second equation is  


    y = 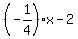,   or

    4y = -x - 8,   or, equivalently,

    4y + x = -8.    (4)



Thus your system is  (2) and (4)

     y = 4x - 19.    (2')

     4y + x = -8.    (4')


Having it in this form, you may transform this system to any other equivalent form you want.