|
Question 1144181: Suppose that the height (in centimeters) of a candle is a linear function of the amount of time (in hours) it has been burning. After 8
hours of burning, a candle has a height of 28.4
centimeters. After 20
hours of burning, its height is 26
centimeters. What is the height of the candle after 11
hours?
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website! Points (x,y):
(8,28.4) and (20,26)
Simplify and solve for y in terms of x.
For the question, substitute 11 for x, and evaluate.
Answer by ikleyn(52781)  (Show Source):
You can put this solution on YOUR website! .
In 12 hours of burning, from 8 hours to 20 hours, the height of the candle decreases by 28.4 - 26 = 2.4 cm.
Thus the height decreases 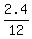 = 0.2 cm per hour.
11 hours after burning start, the height of the candle was (! 3 hours after 8 hours mark !) 28.4 - 0.2*3 = 27.8 cm.
ANSWER. The height of the candle after 11 hours of burning is/was 27.8 cm.
---------------
If you want to see many other similar solved problems, look into the lesson
- Burning candles
in this site.
/\/\/\/\/\/\/\/
Such problems are always easier to solve via their physical meaning than using formal formulas.
It is also much more promising/perspective/solid educational strategy.
First, the students may start earlier solving such problems: at their 5-th or 6-th grades level,
instead of 7-th or 8-th grade with formal formulas.
Second, the students may develop, apply and use their physical intuition and their common sense.
Third, it is the way to exercise their mind and make it more flexible (and more powerful !)
It is why I ALWAYS prefer using a meaningful context against a formal approach while solving such problems.
And only when the students at their 5-th and 6-th grades will learn on how to solve such problems based on their meaningful context,
the time will come, when they can learn it on the next level via using formal formulas - but then they will not come
to this forum for our help -- they will be able to do it on their own (!) -- which is a dream of any tutor/teacher.
One more time, let me repeat my major idea, again:
For such problems, the subject of teaching is to teach students solve the problems at the meaningful level.
At the formal formulas level, there is NO subject to teach, at all : it is entirely mechanical work.
It is just not about solving meaningful problems: it is entirely about using linear interpolation or extrapolation formulas.
|
|
|
| |
