|
Question 1137793: Graph the linear system from problems 1 and 2. Begin by completing the table below, and explain how the graph shows the reasonableness of your solutions to problems 1 and 2
4x - y =5 and 4x -4y = -4
x,y x,y
0 0
1 1
3 -1
I have to find the numbers for y. I would appriciate your help.
Found 2 solutions by ankor@dixie-net.com, MathLover1:
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Graph the linear system from problems 1 and 2. Begin by completing the table below, and explain how the graph shows the reasonableness of your solutions to problems 1 and 2
:
Put the equations in slope intercept form
1.
4x - y = 5
-y = -4x + 5
y should be positive, multiply equation by -1
y = 4x - 5
Now it's easy to make the table
x | y
-------
0 | -5; when x=0, y has to be -5
1 | -1; 4(1) - 5
3 | 7; 4(3) - 5
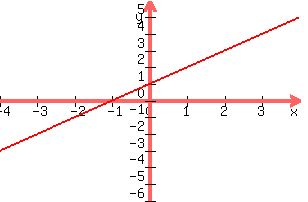
Graph:

:
:
2.
4x - 4y = -4
simplify, divide by 4
x - y = -1
-y = -x - 1
multiply by -1
y = x + 1
:
x | y
-------
0 | 1; substitute 0 for x, find y
1 | 2; substitute 1 for x, " "
-1 | 0; substitute -1 for x, " "
Graph
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
 , ,
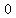 , , -> ->  -> ->  -> ->
 , , -> ->  -> ->  -> ->
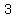 , , -> ->  -> ->  -> ->
and 
 , ,
 , , -> -> -> -> -> -> -> ->
 , , -> -> -> -> -> -> -> ->
 , , -> -> -> -> -> -> -> ->
plot the points for each line and draw lines through

Your two lines make up a system of equations. If the graphs of the equations intersect, then there is one solution that is true for both equations.
When the lines intersect, the point of intersection is the only point that the two graphs have in common.
as you can see from the graph, this system of the equation have a solution, line intersect each other in a point ( , , ) )
|
|
|
| |