|
Question 1132356: Old McDonald is told that he has a total of 20 chickens and cows his hired hand also tells him that there are 64 legs of chickens and cows. How many of each are there
Found 2 solutions by ankor@dixie-net.com, ikleyn:
Answer by ankor@dixie-net.com(22740)   (Show Source):
You can put this solution on YOUR website! Old McDonald is told that he has a total of 20 chickens and cows
a + b = 20
his hired hand also tells him that there are 64 legs of chickens and cows.
2a + 4b = 64
Simplify,divide by 2
a + 2b = 32
How many of each are there
subtract the 1st equation from the above equation
a + 2b = 32
a + b = 20
---------------subtraction eliminates a, find b
0 + b = 12 cows
then
20 - 12 = 8 chickens
;
:
See if that checks out
2(8) + 4(12) =
16 + 48 = 64
Answer by ikleyn(52781)  (Show Source):
You can put this solution on YOUR website! .
Actually, it is an entertainment problem, and a good style and a tradition requires it to be solved by a special method.
One line solution
The number of cows = 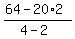 =  = 12. ANSWER: 12 cows.
The rest 20 - 12 = 8 are chickens. ANSWER: 8 chickens.
Check. 8*2 + 12*4 = 64 legs. ! Correct !
Explanation to the one line solution
There is no need to explain that each chicken has 2 legs, while each cow has 4 legs.
Let assume for a minute that all creatures in this problem have 2 legs each.
Then the total number of legs would be 2*20 = 40.
But we are given 64 legs.
The shortage of 64-40 = 24 legs occurred because we assumed and counted only 2 legs for each cow, same as for each chicken.
So we need to fix our calculations, by returning 2 legs with each cow.
Therefore, we divide 64-40 = 24 legs by 2 = (4-2), exactly as the "one line formula" does it, and obtain
our answer - the number of cows - in this way.
Solved.
-------------------
It is totally legal solution. // I mean - it is not a joke !
See the lessons
- Problem on two-wheel and three-wheel bicycles
- Problem on animals at a farm
- Problem on pills in containers
- What type of problems are these?
in this site and find there many other similar problems solved by the same method.
This method is applicable to traditional coin problems; to standard ticket problems; and even to traditional and standard
mixture problems.
It works in this problem and in all mentioned problems in an equal basis with the true Algebra methods, such as
reducing to a single linear equation or reducing to systems of linear equations.
Moreover, when you will learn Algebra more, you will understand and will recognize that this "one line formula" is nothing else
as the solution by the determinant method, which is the same as the Cramer's rule.
So, this "one line formula" is simply a shortcut for these more complicated methods.
Armed with the logic of this solution, you will be able to solve many similar problems even without using equations
(practically MENTALLY) with this shortcut formula, and the logic will lead you and will prevent you of making errors,
when you use this "one line formula" method.
In this way, through the given entertainment problem you get better understanding Algebra, as well as the fast solution method
in your hands.
It is why I wrote this post.
|
|
|
| |
