|
Question 1123708: A school has just purchased new computer equiptment for $25,000.00. The graph shows the desciption of the equiptment over 5 years. The point (0, 25,000) represents the purchase price and the point (5,0) represents when the equiptment will be replaced. Write a linear equation in slope-intercept form that models the value of the equiptment, y, x years after purchase. Use the model to predict the value of the equiptment after 2 year?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the point (0,2500) says the value of y = 25000 when the value of x is equal to 0.
x represents the number of years since the computer was purchased.
y represents the depreciated value of the computer after x years.
the point (5,0) says the value of y = 25000 when the value of x is 5.
this means the depreciated value of the computer is 0 after 5 years.
with straight line depreciation, the same value is subtracted from the computer every year the computer is in use.
the computer goes from 25,000 to 0 in 5 years.
25,000 / 5 = a depreciation value of 5000 each year.
the slope intercept form of a linear equation is y = mx + b
m is the slope
b is the y-intercept.
if the value of the computer goes down every year, than the slope is -5000.
the slope is the change in the value of y for every change in the value of x.
a slope of -5000 is the same as a slope of -5000 / 1
that says the value of y goes down 5000 for every increase of 1 in the value of x.
the euatin becomes y = -5000 * x + b
to solve for b, you need a point on the line.
(0,25000) is one point on the line.
(5,0) is the other point on the line.
i'll use (5,0).
you can use (0,25000) yourself to see that you'll get the same value of b.
when you use the point (5,0), y = -5000 * x + b becomes 0 = -5000 * 5 + b
you replace x with 5 and you replace y with 0 to solve for b.
0 = -5000 * 5 + b becomes 0 = -25000 + b
solve for b to get b = 25000.
the equation becomes y = -5000 * x + 25000
this is your linear equation in slope intercept form.
at the end of 2 years, the equation becomes y = -5000 * 2 + 25,000, which results in y = 15,000
the depreciated value of the computer is 15,000 after 2 years.
the equation can be graphed as shown below:
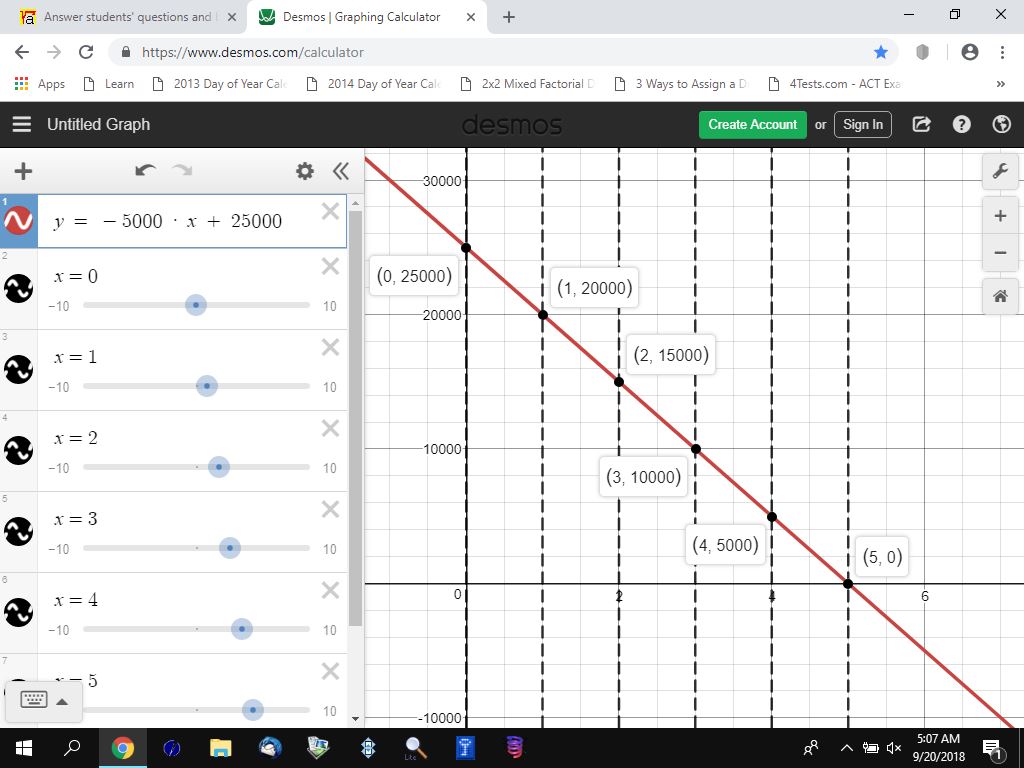
the red line is the line of the equation of y = -5000 * x + 25000.
the vertical dashed lines are just there to allow me to show the intersection points of the depreciated value of the computer after x years.
|
|
|
| |