SOLUTION: 85 tickets were sold for $2105. The number of reserved tickets sold was one more than twice as many as the number of premium tickets sold. If premium seats cost $39, reserved seat

Algebra ->  Linear-equations -> SOLUTION: 85 tickets were sold for $2105. The number of reserved tickets sold was one more than twice as many as the number of premium tickets sold. If premium seats cost $39, reserved seat      Log On


   

Question 1115539: 85 tickets were sold for $2105. The number of reserved tickets sold was one more
than twice as many as the number of premium tickets sold. If premium seats cost $39, reserved seats cost $29 and general admission seats cost $19, how many tickets of each kind were sold?
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
x    general   19
y    reserved  29
z    premium   39

system%28x%2By%2Bz=85%2Cy=2z%2B1%2C19x%2B29y%2B39z=2105%29

system%28x%2B2z%2B1%2Bz=85%2C19x%2B29%282z%2B1%29%2B39z=2105%29

x%2B3z=84

-

19x%2B58z%2B29%2B39z=2105
19x%2B97z=2105-29
19x%2B97z=2076


system%28x%2B3z=84%2C19x%2B97z=2076%29

system%2819x%2B57z=1596%2C19x%2B97z=2076%29

40z=480
highlight%28z=12%29-------premium tickets sold.

Evaluate the others.

Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.
Let P be the number of premium tickets.

Then the number of reserved tickets is (2P+1).

Then the number of general admission seats is  (85 - P - (2P+1)) = (84-3P).


The "money" equation is

39*P + 29*(2P+1) + 19*(84-3P) = 2105


39*P + 58*P - 57*P + 29 + 19*84 = 2105

40*P = 2105 - 29 - 19*84 = 480  ====>  P = 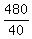480%2F40 = 12  premium tickets.



====>  # of reserved tickets = 2P+1 = 25.  # of the general admission seats = 84 - 3*12 = 48.



Answer.  12 premium,  25 reserved and  48 general admission.


Check.   12 + 25 + 48 = 85;   12*39 + 25*29 + 48*19 = 2105 dollars.   ! Correct !

Solved.

==============

The lesson to learn from this solution: 

     This problem is for ONE unknown.

     It is not for using the systems of equations.

     Your major task is to select the basic unknown by reasonable/rational way,

          then to express other unknowns via that basic variable and to built/to construct the equation to solve.

     Learn from those in this forum who knows the subject and ignore those who does not know.

===================

To see other similar problems solved in this way,  look into the lessons
    - More solved word problems on a single linear equation
in this site.