Question 1115405: Find the point dividing the interval AB in the ratio 1:3 if A(-1,1) and B is (3,-1)
Answer by MathLover1(20849)   (Show Source):
You can put this solution on YOUR website! Find the point dividing the interval AB in the ratio  if A( , ) and B is ( ,)
To find the point  that divides a segment  into a particular ratio, determine the ratio  by writing the numerator over the sum of the numerator and the denominator of the given ratio.
Next, find the rise and the run (slope) of the line. Finally, add times the run to the  -coordinate of  and add times the rise to the  -coordinate of .
This process is summarized with the following formula:
P(,)=( ,  )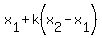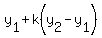
you have:
A(,) =>  , 
and
B is (,) =>  , 
(,)=( ,  )
(,)=( ,  )
(,)=( ,  )
(,)=( ,  )
(,)=( , )
|
|
|
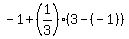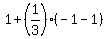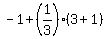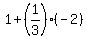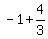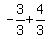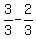