SOLUTION: If A (2,5), B(-3,10) and C (-5,2) are vertices of a triangle, find its area

Algebra ->  Linear-equations -> SOLUTION: If A (2,5), B(-3,10) and C (-5,2) are vertices of a triangle, find its area       Log On


   

Question 1115402: If A (2,5), B(-3,10) and C (-5,2) are vertices of a triangle, find its area
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!

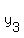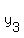The area of a triangle with vertices (x%5B1%5D,y%5B1%5D), (x%5B2%5D,y%5B2%5D), (x%5B3%5D,y%5B3%5D) is:



In this case, A (2,5)=(x%5B1%5D,y%5B1%5D), B(-3,10)=(x%5B2%5D,y%5B2%5D) and C (-5,2)=(x%5B3%5D,y%5B3%5D), we have


A+=+%2820%2B15+-6+%2B50+-25+-+4%29+%2F+2
A+=+50+%2F+2
A+=+25

A similar formula can be used to find the area of any polygon.
If you prefer not to use this formula, then another method is to use Distance Formula to find the length of each side:
side AB, AC, and BC
if
A (2,5)
B(-3,10)
C (-5,2)
AB=%28x%5B1%5D-x%5B2%5D%29%5E2%2B%28y%5B1%5D-y%5B2%5D%29%5E2
AB=+sqrt%282-%28-3%29%29%5E2%2B%285-10%29%5E2%29
AB=+sqrt%282%2B3%29%5E2%2B%28-5%29%5E2%29
AB=sqrt%285%5E2%2B%28-5%29%5E2%29
AB=sqrt%2825%2B25%29
AB=sqrt%282%2A25%29
AB=5sqrt%282%29
AB=7.1+

AC=%28x%5B1%5D-x%5B2%5D%29%5E2%2B%28y%5B1%5D-y%5B2%5D%29%5E2
AC=+sqrt%282-%28-5%29%29%5E2%2B%285-2%29%5E2%29
AC=+sqrt%282%2B5%29%5E2%2B3%5E2%29
AC=sqrt%287%5E2%2B3%5E2%29
AC=sqrt%2849%2B9%29

AC=sqrt%2858%29
AC=7.6


BC=%28x%5B1%5D-x%5B2%5D%29%5E2%2B%28y%5B1%5D-y%5B2%5D%29%5E2
BC=+sqrt%28-3-%28-5%29%29%5E2%2B%2810-2%29%5E2%29
BC=+sqrt%282%5E2%2B8%5E2%29
BC=+sqrt%2868%29
BC=+8.25



since you have scalene triangle (no equal sides), you can also calculate the area from the lengths of all three sides using Heron's Formula
Calculate "s" (half of the triangles perimeter):
s+=+%28a%2Bb%2Bc%29%2F2
s+=+%287.1%2B7.6%2B8.25%29%2F2
s+=+11.475
Then calculate the Area:
A+=sqrt%28s%28s-AB%29%28s-AC%29%28s-BC%29%29
A+=sqrt%2811.475%2811.475-7.1%29%2811.475-7.6%29%2811.475-8.25%29%29
A+=25.0476 round it to whole number
A+=25