SOLUTION: Hi, Please help me to solve step-by-step on these questions. Thank you very much. 10. Explain in words how to determine whether : nth root of a^n = a Or nth root of

Algebra ->  Linear-equations -> SOLUTION: Hi, Please help me to solve step-by-step on these questions. Thank you very much. 10. Explain in words how to determine whether : nth root of a^n = a Or nth root of       Log On


   

Question 1112786: Hi,
Please help me to solve step-by-step on these questions.
Thank you very much.
10. Explain in words how to determine whether :

nth root of a^n = a
Or
nth root of a^n = /a/
Simplify the following expression by first rewriting to remove the negative exponent, then writing in radical form, then evaluating, and final simplifying. Refer to Section 8.2 in the text.
(-27)/64)^(-2/3)
Found 3 solutions by Boreal, KMST, ikleyn:
Answer by Boreal(15235) About Me  (Show Source):
You can put this solution on YOUR website!
n th root of a term, n being even, is the absolute value.
The presence of the radical asks for the positive square root.
For the second, invert the fraction to remove the negative sign of the exponent.
(-64/27)^(2/3)=cube root of each squared. That becomes (-4/3)^2 or 16/9.

Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
It depends on what you know about a and n.
If you are given values for a and n it is easy:

If a%3E=0 and n is a positive integer, root%28n%2Ca%5En%29=a .
Example #1: for a=2 and n=7 , root%287%2C2%5E7%29=root%287%2C128%29=2 .
Example #2: for a=3 and n=4 , root%286%2C3%5E4%29=root%284%2C81%29=3 .

If a%3C0 and n is an even (positive) integer, root%28n%2Ca%5En%29=abs%28a%29 .
Example #3: for a=-5 and n=4 , root%284%2C%28-5%29%5E4%29=root%284%2C625%29=5 .

If a%3C0 and n is an odd (positive) integer, root%28n%2Ca%5En%29=a .
Example #3: for a=-5 and n=3 , root%283%2C%28-5%29%5E3%29=root%284%2C-125%29=-5 .


IF YOU DO NOT HAVE ENOUGH INFORMATION:
If n is an even (positive) integer, root%28n%2Ca%5En%29=abs%28a%29 is always true.
root%284%2C%28-5%29%5E4%29=root%284%2C625%29=5=abs%28-5%29 and root%284%2C5%5E4%29=root%284%2C625%29=5=abs%28-5%29 .

If n is an odd (positive) integer, root%28n%2Ca%5En%29=a is always true.
root%283%2C%28-5%29%5E43%29=root%284%2C-125%29=-5 and root%283%2C5%5E3%29=root%284%2C125%29=5 .

By definition of negative exponent, 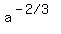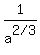a%5E%28-%222+%2F+3%22%29%22=%221%2Fa%5E%222+%2F+3%22 ,
and 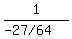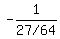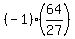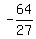1%2F%22-27+%2F+64%22%22=%22-1%2F%2227+%2F+64%22%22=%22%28-1%29%2864%2F27%29%22=%22-64%2F27 as you already knew.
You probably would just write as one step: 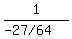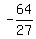1%2F%22-27+%2F+64%22%22=%22-64%2F27 .

Putting that old and new knowledge together, what you are probably expected to write is
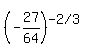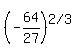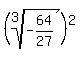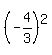
%28-27%2F64%29%5E%22-+2+%2F+3%22%22=%22%28-64%2F27%29%5E%222+%2F+3%22%22=%22%28root%283%2C-64%2F27%29%29%5E2%29%22=%22%28-4%2F3%29%5E2%22=%22%2816%2F9%29

Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.
What is sqrt%28x%29, it is heavily depends on context.


The reason is that sqrt%28x%29, taken as is, is not a single function or a single value.


sqrt%284%29 has, strongly speaking, two values, 2 and -2.


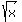sqrt%28x%29 as a function,  has, strongly speaking, two branches,  | sqrt%28x%29%29 |  and  -| sqrt%28x%29 |.  


In other words, there are TWO different functions practically under the same name.


So, without the context,  sqrt%28x%29  is not a single value or a function. 
In opposite, it is THE SET of two values or two functions.


Only if and when the context is EXPLICITLY (or IMPLICITLY) DEFINED, it becomes one function or one single value.


Professional mathematicians "feel" the context practically with no error, but for the school people (students or/and teachers) 
it is often difficult to feel the context.


Therefore in school Math nobody and never explains it, because this understanding gains only with experience.