SOLUTION: Hi, Please help me to solve step-by-step on these questions. Thank you very much. 3. Factor the following polynomial by Grouping : (Show all work) Explain how to know when to f

3) 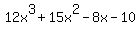  = group the terms =  -  =  -  = .


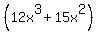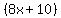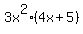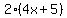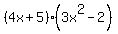    Done.

4)  What are the steps to find the domain of a rational function ?


    Answer.  

    A rational function is the ratio of two polynomials.

    To find the domain of the rational function, you need

        a) to consider its DENOMINATOR.

        b) to find the roots of the polynomial in the denominator

              (that make the denominator equal to zero !)

        c) then exclude these roots from the set of all real numbers (from the number line).

           The remained set of real numbers is the domain of the given rational function.


    In your case, you need to consider the denominator 2x^3-x^2-x.


    It is the polynomial of the third degree.

    You can factor it in this way  2x^3-x^2-x = x*(2x^2 - x -1) = x*(2x+1)*(x-1).

    The roots are  x= 0,  x= -1/2  and  x= 1.


     So, the domain of the given rational function is the set of all real numbers except -1/2, 0 and 1  (listed in ascending order).