|
Question 1111745: Find the perpendicular distance between the line y=(5/13)x + 5 and the origin.
Found 2 solutions by math_helper, KMST:
Answer by math_helper(2461)   (Show Source): (Show Source):
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Distance from a point to a line is always measured along a perpendicular, of course.
If you were at point P in the sketch below,along what path would you measure your distance to the pool?
 along what path would you measure your distance to the pool, d, e, or f? along what path would you measure your distance to the pool, d, e, or f?
MY GUESS AS TO THE EXPECTED SOLUTION:
Your teacher (or textbook) has probably given you the formula
to calculate the distance between a point 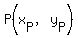
and a line with equation  as as
  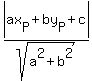 . .
In this case, your point is the origin  , ,
so  , and , and
 can be transformed, can be transformed,
by rearranging and multiplying both sides of the equal sign time  , ,
to get the equivalent equation
 , with , with  , ,  , ,  . .
So, in this case,
  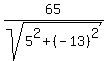 } } 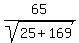 } }  . .
The elegant way to express the exact value is

The approximate value for that irrational number
is the never ending, non-repeating, decima 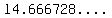 . .
ANOTHER APPROACH:
It is easy to see that the x- and y-intercepts are the points
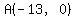 and and 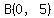 . .
If you look at the line, the axes,
and the path along which you would measure the distance to the origin,
you see right triangles:
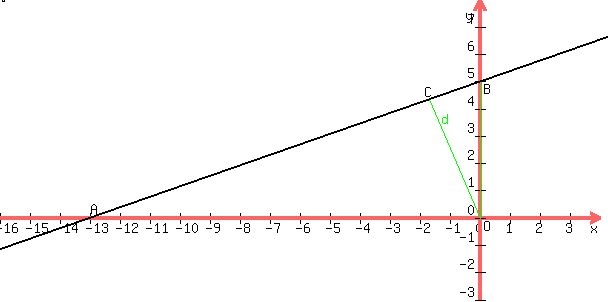
When people see right triangles they think about
trigonometric ratios,
or the Pythagorean theorem,
or similar triangles.
Each of those ideas can also lead to a solution,
as another tutor showed you for trigonometric ratios.
USING THE PYTHAGOREAN THEOREM:
The most obvious right triangle in the sketch above is big triangle ABO ,
with hypotenuse  , ,
calculated using the Pythagorean theorem.
The area of ABO is  , ,
calculated as  , ,
using AO as the base and OB as the height.
As we know that the distance 
is measured along line OC, perpendicular to AB,
we could also calculate the area as  , ,
using  as the base and as the base and  as the height. as the height.
Substituting, and combining both ways of calculating area



USING SIMILAR TRIANGLES:
Triangles ABO and BCO are both right triangles,
and they both have the same angle at B,
so they are similar triangles,
with BCO being a scaled-down version of ABO.
The ratio of corresponding sides is the scale factor,
the same for the long leg as for the hypotenuse
 , so , so
 . .
|
|
|
| |