|
Question 1107674: Determine whether the lines are parallel, perpendicular, or neither.
f(x)= 12x - 6
g(x)= -12x + 11
f(x) = 14x - 9
g(x) = 14x + 9
-7x + 28y = 2
-4x - y = 8
-6x + 3y = 2
3x + 6y = 18
x + 5y = -10
5x + 4y = 13
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! Determine whether the lines are parallel, perpendicular, or neither.
Put the listing inside the 'pre' tags and it will look the way you wanted:
f(x)= 12x - 6
g(x)= -12x + 11
f(x) = 14x - 9
g(x) = 14x + 9
-7x + 28y = 2
-4x - y = 8
-6x + 3y = 2
3x + 6y = 18
x + 5y = -10
5x + 4y = 13
You need to know for the slopes:
If same, the parallel.
If negative reciprocals, or their product is negative 1, the perpendicular.
If neither of these, then "neither" but their lines intersect.
Some of you pair are in the slope-intercept form, so you figure those yourself.
Some of your pair are in the AX+By=C form, so you can still find the slope of each by solve for y in terms of x, and adjust to the slope-intercept form: slope would be 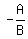 . .
|
|
|
| |