|
Question 1107608: 3x+4y=62 & 5x+2y=52
Found 2 solutions by addingup, ikleyn:
Answer by addingup(3677)   (Show Source): (Show Source):
You can put this solution on YOUR website! 3x+4y=62 & 5x+2y=52
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
5x+2y=52: multiply all times -2 and add to the other equation
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
3x+4y=62
+
-10x-4y= -104
--------------
-7x 0y = -42
-7x = - 42
x = -42/-7 divide to get your answer. Remember that -/- = + so in this case you can ignore the - sign, just divide 42/7 or do it in your head, by now you should know that 42 is the product of 7 x 6
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Now find y, substitute in the original equations:
3x+4y=62; 3(6)+4y = 62; 18+4y = 62; 4y = 44; y = 11
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Check: let's try the answers in the two equations:
3x+4y=62; 3(6)+4(11) = 62; 18+44 = 62 Correct
Now the other equation:
5x+2y=52; 5(6)+2(11) = 52; 30+22 = 52 Also correct.
You now have the correct answers.
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
3x + 4y = 62, (1)
5x + 2y = 52. (2)
To solve the system, I will use the Elimination method. For it, multiply the equation (2) by 2 (both sides).
Keep equation (1) unchanged. You will get
3x + 4y = 62, (1')
10x + 4y = 104. (2')
Now subtract equation (1') from equation {2'). The terms "4y", that are equal in both equations
(that I made equal in both equations) will cancel each other, and you will get a single equation containing only one unknown "x"
10x - 3x = 104 - 62, or
7x = 42.
It is how the Elimination method works.
Now x = 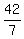 = 6.
So, you just found the value of x= 6.
Now substitute this value into either of the two given/original equations and find y. I will use equation (1):
3*6 + 4y = 62 ====> 4y = 62 - 3*6 = 44 ====> y = = 6.
So, you just found the value of x= 6.
Now substitute this value into either of the two given/original equations and find y. I will use equation (1):
3*6 + 4y = 62 ====> 4y = 62 - 3*6 = 44 ====> y = 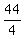 = 11.
Answer. x= 6, y= 11.
Check. Check the solution on your own. = 11.
Answer. x= 6, y= 11.
Check. Check the solution on your own.
|
|
|
| |